题目内容
函数y=2x3+1的图象与函数y=3x2-b的图象有三个不相同的交点,则实数b的取值范围是( )
| A．(-2,-1) | B．(-1,0) |
| C．(0,1) | D．(1,2) |
B
由题意知方程2x3+1=3x2-b,
即2x3-3x2+1=-b有三个不相同的实数根,
令f(x)=2x3-3x2+1,
即函数y=f(x)=2x3-3x2+1与直线y=-b有三个交点.
由f'(x)=6x2-6x=6x(x-1)知,函数y=f(x)在区间(-∞,0)上单调递增,在(0,1)上单调递减,在(1,+∞)上单调递增,故f(0)是函数的极大值,f(1)是函数的极小值,若函数y=f(x)=2x3-3x2+1与直线y=-b有三个交点,则f(1)<-b<f(0),解得-1<b<0.
即2x3-3x2+1=-b有三个不相同的实数根,
令f(x)=2x3-3x2+1,
即函数y=f(x)=2x3-3x2+1与直线y=-b有三个交点.
由f'(x)=6x2-6x=6x(x-1)知,函数y=f(x)在区间(-∞,0)上单调递增,在(0,1)上单调递减,在(1,+∞)上单调递增,故f(0)是函数的极大值,f(1)是函数的极小值,若函数y=f(x)=2x3-3x2+1与直线y=-b有三个交点,则f(1)<-b<f(0),解得-1<b<0.
练习册系列答案
优百分课时互动系列答案
相关题目
．
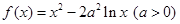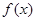在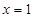
处取得极值，求实数
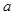的值；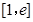
上没有零点，求实数
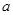的取值范围．
，
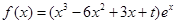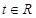.若函数
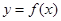依次在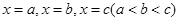
处取到极值.
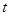的取值范围；
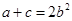，求
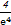
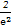
x3＋bx有三个单调区间，则b的取值范围是________．