题目内容
已知函数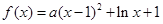 .
.
(1)当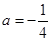 时,求函数
时,求函数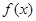 的极值;
的极值;
(2)若函数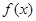 在区间
在区间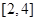 上是减函数,求实数
上是减函数,求实数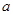 的取值范围;
的取值范围;
(3)当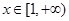 时,函数
时,函数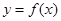 图像上的点都在
图像上的点都在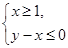 所表示的平面区域内,求实数
所表示的平面区域内,求实数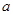 的取值范围.
的取值范围.
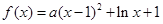 .
.(1)当
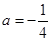 时,求函数
时,求函数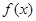 的极值;
的极值;(2)若函数
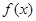 在区间
在区间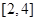 上是减函数,求实数
上是减函数,求实数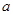 的取值范围;
的取值范围;(3)当
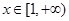 时,函数
时,函数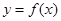 图像上的点都在
图像上的点都在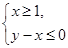 所表示的平面区域内,求实数
所表示的平面区域内,求实数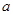 的取值范围.
的取值范围.(1)当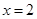 时,函数
时,函数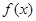 取得极大值
取得极大值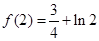 ;(2)
;(2) ;(3)
;(3)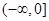 .
.
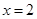 时,函数
时,函数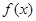 取得极大值
取得极大值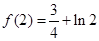 ;(2)
;(2) ;(3)
;(3)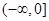 .
.试题分析:(1)将
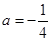 代入函数解析式,直接利用导数求出函数
代入函数解析式,直接利用导数求出函数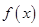 的单调递增区间和递减区间,从而可确定函数
的单调递增区间和递减区间,从而可确定函数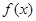 的极值;(2)将条件“
的极值;(2)将条件“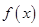 在区间
在区间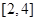 上为减函数”等价转化为“不等式
上为减函数”等价转化为“不等式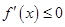 在区间
在区间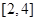 上恒成立”,结合参数分离法进一步转化为
上恒成立”,结合参数分离法进一步转化为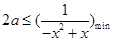 ,从中根据二次函数的图像与性质求出
,从中根据二次函数的图像与性质求出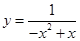 在
在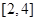 上的最小值即可解决本小问;(3)因函数
上的最小值即可解决本小问;(3)因函数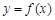 图像上的点都在
图像上的点都在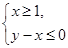 所表示的平面区域内,则当
所表示的平面区域内,则当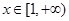 时,不等式
时,不等式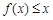 恒成立,即
恒成立,即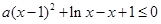 恒成立,设
恒成立,设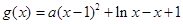 (
(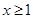 ),只需
),只需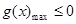 即可,转化思想的运用.
即可,转化思想的运用.试题解析:(1)当
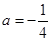 时,
时,
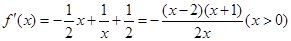
由
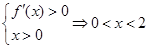 ,由
,由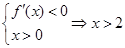
故当
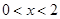 时,
时,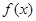 单调递增;当
单调递增;当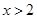 时,
时,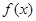 单调递减
单调递减所以当
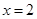 时,函数
时,函数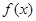 取得极大值
取得极大值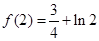 4分
4分(2)
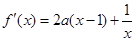 ,∵函数
,∵函数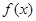 在区间
在区间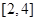 上单调递减
上单调递减∴
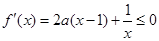 在区间
在区间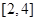 上恒成立,即
上恒成立,即 在
在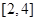 上恒成立,只需
上恒成立,只需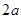 不大于
不大于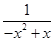 在
在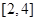 上的最小值即可 6分
上的最小值即可 6分而
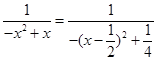
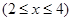 ,则当
,则当 时,
时,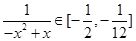
∴
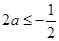 ,即
,即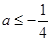 ,故实数
,故实数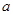 的取值范围是
的取值范围是 . 8分
. 8分(3)因
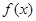 图像上的点在
图像上的点在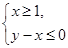 所表示的平面区域内,即当
所表示的平面区域内,即当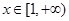 时,不等式
时,不等式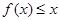 恒成立,即
恒成立,即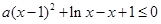 恒成立,设
恒成立,设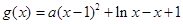 (
(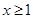 ),只需
),只需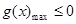 即可.
即可.由
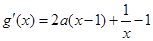
 ,
,(ⅰ)当
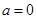 时,
时,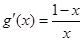 ,当
,当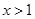 时,
时,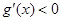 ,函数
,函数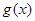 在
在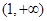 上单调递减,故
上单调递减,故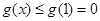 成立. 9分
成立. 9分(ⅱ)当
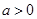 时,由
时,由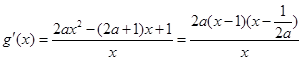 ,令
,令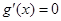 ,得
,得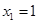 或
或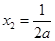 ,
, ①若
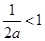 ,即
,即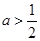 时,在区间
时,在区间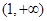 上,
上,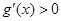 ,函数
,函数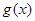 在
在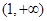 上单调递增,函数
上单调递增,函数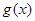 在
在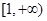 上无最大值,不满足条件;
上无最大值,不满足条件;②若
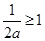 ,即
,即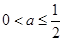 时,函数
时,函数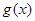 在
在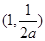 上单调递减,在区间
上单调递减,在区间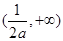 上单调递增,同样
上单调递增,同样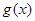 在
在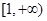 上无最大值,不满足条件. 11分
上无最大值,不满足条件. 11分(ⅲ)当
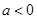 时,由
时,由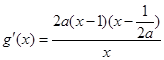 ,因
,因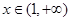 ,故
,故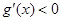 ,则函数
,则函数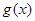 在
在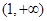 上单调递减,故
上单调递减,故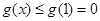 成立.
成立.综上所述,实数
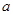 的取值范围是
的取值范围是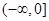 . 12分
. 12分
练习册系列答案
相关题目
 ,
,  的单调区间;
的单调区间; 内存在
内存在 ,使不等式
,使不等式 成立,求
成立,求 的取值范围.
的取值范围.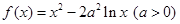 .
.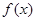 在
在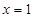 处取得极值,求实数
处取得极值,求实数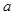 的值;
的值;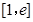 上没有零点,求实数
上没有零点,求实数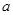 的取值范围.
的取值范围.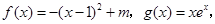 若
若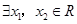 ,使得
,使得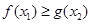 成立,则实数
成立,则实数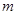 的取值范围是_______.
的取值范围是_______.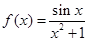 .下列命题:( )
.下列命题:( )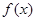 的图象关于原点对称; ②函数
的图象关于原点对称; ②函数 时,函数
时,函数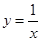 的图象没有公共点,其中正确命题的序号是
的图象没有公共点,其中正确命题的序号是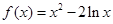 的单调递减区间是____________________.
的单调递减区间是____________________. 的单调递增区间是
的单调递增区间是