题目内容
已知函数f(x)=logax+x-b(a>0,且a≠1).当2<a<3<b<4时,函数f(x)的零点x0∈(n,n+1),n∈N*,则n=______.
设函数y=logax,m=-x+b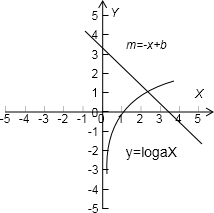
根据2<a<3<b<4,
对于函数y=logax在x=2时,一定得到一个值小于1,
在同一坐标系中划出两个函数的图象,判断两个函数的图形的交点在(2,3)之间,
∴函数f(x)的零点x0∈(n,n+1)时,n=2,
故答案为:2
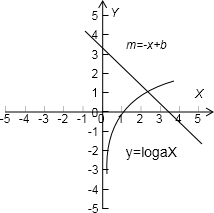
根据2<a<3<b<4,
对于函数y=logax在x=2时,一定得到一个值小于1,
在同一坐标系中划出两个函数的图象,判断两个函数的图形的交点在(2,3)之间,
∴函数f(x)的零点x0∈(n,n+1)时,n=2,
故答案为:2

练习册系列答案
相关题目







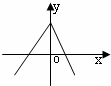





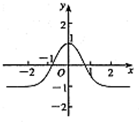
 在
在 上的图像大致为( )
上的图像大致为( )
