题目内容
如图，半径为1的半圆O与等边三角形ABC夹在两平行线l1，l2之间，l∥l1，l与半圆相交于F，G两点，与三角形ABC两边相交于E，D两点．设弧
的长为x（0＜x＜π），y=EB+BC+CD，若l从l1平行移动到l2，则函数y=f（x）的图象大致是（ ）
 |
| FG |
A． | B． | C． | D． |
当x=0时，y=EB+BC+CD=BC=
；
当x=π时，此时y=AB+BC+CA=3×
=2
；
当x=
时，∠FOG=
，三角形OFG为正三角形，此时AM=OH=
，
在正△AED中，AE=ED=DA=1，
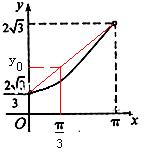∴y=EB+BC+CD=AB+BC+CA-（AE+AD）=3×
-2×1=2
-2．如图．
又当x=
时，图中y0=
+
（2
-
）=
＞2
-2．
故当x=
时，对应的点（x，y）在图中红色连线段的下方，对照选项，D正确．
故选D．
2
| ||
| 3 |
当x=π时，此时y=AB+BC+CA=3×
2
| ||
| 3 |
| 3 |
当x=
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
在正△AED中，AE=ED=DA=1，
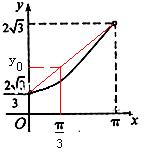∴y=EB+BC+CD=AB+BC+CA-（AE+AD）=3×2
| ||
| 3 |
| 3 |
又当x=
| π |
| 3 |
2
| ||
| 3 |
| 1 |
| 3 |
| 3 |
2
| ||
| 3 |
10
| ||
| 9 |
| 3 |
故当x=
| π |
| 3 |
故选D．
练习册系列答案
口算与应用题卡系列答案
名师点睛字词句段篇系列答案
相关题目
