题目内容
【题目】某中学为弘扬优良传统，展示80年来的办学成果，特举办“建校80周年教育成果展示月”活动。现在需要招募活动开幕式的志愿者，在众多候选人中选取100名志愿者，为了在志愿者中选拔出节目主持人，现按身高分组，得到的频率分布表如图所示.
（1）请补充频率分布表中空白位置相应数据，再在答题纸上完成下列频率分布直方图；
（2）为选拔出主持人，决定在第3、4、5组中用分层抽样抽取6人上台，求第3、4、5组每组各抽取多少人？
（3）在（2）的前提下，主持人会在上台的6人中随机抽取2人表演诗歌朗诵，求第3组至少有一人被抽取的概率？
参考公式：
.
【答案】（1）见解析； （2）3,2,1； （3）
.
【解析】
（1）根据频率、频数与样本容量的关系，求出对应的数值，画出频率分布直方图；
（2）利用分层抽样原理，求出各小组应抽取的人数；
（3）利用列举法求出基本事件数，计算对应的概率值．
(1)第二组的频数为
，故第三组的频数为
，故第三组的频率为0.3，第五组的频率为0.1，补全后频率分布表为：
组号 | 分组 | 频数 | 频率 |
第一组 |
|
| 0.05 |
第二组 |
|
| 0.35 |
第三组 |
|
| 0.3 |
第四组 |
|
| 0.2 |
第五组 |
|
| 0.1 |
合计 | 100 | 1 |
频率分布直方图为：
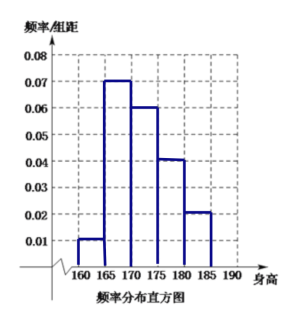
（2）第三组、第四组、第五组的频率之比3:2:1，
故第三组、第四组、第五组抽取的人数分别为3,2,1.
（3）设第三组中抽取的三人为
，第四组中抽取的两人为
，第五组中抽取的一人为C，则6人中任意抽取两人，所有的基本事件如下：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，
故第三组中至少有1人被抽取的概率为
.
练习册系列答案
相关题目
