题目内容
【题目】已知椭圆![]() 的离心率为
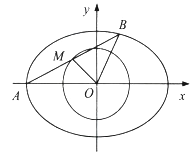
的离心率为![]() ,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为2。
,过右焦点F的直线l与C相交于A、B两点,当l的斜率为1时,坐标原点O到l的距离为2。
(1)求椭圆C的方程;
(2)椭圆C上是否存在一点P,使得当l绕F转到某一位置时,有![]() 成立?若存在,求点P的坐标与直线l的方程;若不存在,说明理由。
成立?若存在,求点P的坐标与直线l的方程;若不存在,说明理由。
【答案】(1)![]() ; (2)
; (2)![]() ,直线
,直线![]() ,或
,或![]() ,直线
,直线![]() .
.
【解析】
(1) 设![]() ,可得直线l的方程为
,可得直线l的方程为![]() ,运用点到直线距离公式,可求出c,再由离心率公式即可求出a,b从而可得椭圆方程;
,运用点到直线距离公式,可求出c,再由离心率公式即可求出a,b从而可得椭圆方程;
(2) 设![]() ,
,![]() ,
,![]() , 设
, 设![]() 代入椭圆方程消元,再由韦达定理和向量的坐标运算,求出点P的坐标,代入椭圆方程,即可求出结果.
代入椭圆方程消元,再由韦达定理和向量的坐标运算,求出点P的坐标,代入椭圆方程,即可求出结果.
(1)设![]() ,可得直线l的方程为
,可得直线l的方程为![]() ,
,
即为![]() ,由坐标原点O到l的距离为2,
,由坐标原点O到l的距离为2,
即有![]() ,解得
,解得![]() ,
,
由![]() ,可得
,可得![]() ,b=2,
,b=2,
即有椭圆的方程为![]() ;
;
(2)设![]() ,
,![]() ,
,![]() ,
,
①当直线![]() 的斜率存在,设其方程为:
的斜率存在,设其方程为:![]()
由![]() ,消去y得
,消去y得![]() .
.
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
将P点坐标代入椭圆得![]() ,
,
∴![]() ,∴
,∴![]() (
(![]() 舍去),即为
舍去),即为![]() .
.
当![]() 时,
时,![]() ,直线
,直线![]() ,
,
当![]() 时,
时,![]() ,直线
,直线![]() .
.
②当直线![]() 的斜率不存在时,直线
的斜率不存在时,直线![]() 的方程为:
的方程为:![]() ,
,
依题意,四边形OAPB为菱形,此时点P不在椭圆上,
即当直线![]() 的斜率不存在时,不适合题意;
的斜率不存在时,不适合题意;
综上所述,存在P,且![]() ,直线
,直线![]() ,
,
或![]() ,直线
,直线![]() .
.

练习册系列答案
相关题目