题目内容
【题目】已知双曲线方程为![]() .
.
(1)求以定点![]() 为中点的弦所在的直线方程;
为中点的弦所在的直线方程;
(2)以定点![]() 为中点的弦存在吗?若存在,求出其所在的直线方程;若不存在,请说明理由.
为中点的弦存在吗?若存在,求出其所在的直线方程;若不存在,请说明理由.
【答案】(1)![]() ;(2)不存在,理由见解析
;(2)不存在,理由见解析
【解析】
(1)设以定点![]() 为中点的弦的端点坐标为
为中点的弦的端点坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,运用中点坐标公式和直线的斜率公式,运用点差法可得所求直线的斜率,再由点斜式方程即可得到所求直线方程;
,运用中点坐标公式和直线的斜率公式,运用点差法可得所求直线的斜率,再由点斜式方程即可得到所求直线方程;
(2)假设定点![]() 为中点的弦存在,设以定点
为中点的弦存在,设以定点![]() 为中点的弦的端点坐标为
为中点的弦的端点坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,运用中点坐标公式和直线的斜率公式,结合点差法,求得直线的斜率,由点斜式方程可得直线方程,代入双曲线的方程,检验判别式是否大于0,即可判断是否存在.
,运用中点坐标公式和直线的斜率公式,结合点差法,求得直线的斜率,由点斜式方程可得直线方程,代入双曲线的方程,检验判别式是否大于0,即可判断是否存在.
解:(1)设以定点![]() 为中点的弦的端点坐标为
为中点的弦的端点坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可得![]() ,
,![]() ,①
,①
由端点在双曲线上,可得![]() ,
,![]() ,
,
两式相减可得![]() ,
,
将①代入上式,
可得以定点![]() 为中点的弦所在的直线斜率为
为中点的弦所在的直线斜率为
![]() ,
,
则以定点![]() 为中点的弦所在的直线方程为
为中点的弦所在的直线方程为![]() ,
,
即为![]() ,
,
代入双曲线的方程可得![]() ,
,
由![]() ,可得所求直线存在,
,可得所求直线存在,
即有所求直线的方程为![]() ;
;
(2)假设定点![]() 为中点的弦存在,
为中点的弦存在,
设以定点![]() 为中点的弦的端点坐标为
为中点的弦的端点坐标为![]() ,
,![]() ,
,![]() ,
,![]() ,
,
可得![]() ,
,![]() ,②
,②
由端点在双曲线上,可得![]() ,
,![]() ,
,
两式相减可得![]() ,
,
将②代入上式,
可得以定点![]() 为中点的弦所在的直线斜率为
为中点的弦所在的直线斜率为
![]() ,
,
则以定点![]() 为中点的弦所在的直线方程为
为中点的弦所在的直线方程为![]() ,
,
即为![]() ,
,
代入双曲线的方程可得![]() ,
,
由![]() ,可得所求直线不存在,
,可得所求直线不存在,
以定点![]() 为中点的弦不存在.
为中点的弦不存在.

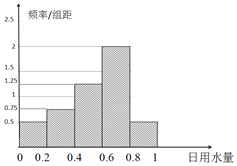
【题目】为达到节水节电的目的,某家庭记录了20天的日用电量xi(单位:度)的频数分布表和这20天相应的日用水量yi(单位:m3)的频率分布直方图如下:
日用电量xi | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) |
频数(天) | 2 | 5 | 7 | 3 | 3 |
(1)假设水费为2.5元/m3,电费为0.6元/度,用以上数据估计该家庭日用电量的平均值和日用水量的平均值,并据此估计该家庭一个月的水费和电费一共是多少?(一个月按30天算,同一组中的数据以这组数据所在区间中点的值作代表);
(2)假设该家庭的日用水量y和日用电量x可用线性回归模型来拟合,请利用(1)中的计算数据及所给的参考数据和公式,建立y与x的回归方程,预测若该家庭日用电量为20度时的日用水量是多少m3?(回归方程的系数小数点后保留2位小数)
参考数据:![]() xiyi=65,
xiyi=65,![]() 612
612
参考公式:回归方程![]() x
x![]() 中斜率和截距的公式分别为:
中斜率和截距的公式分别为:
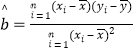 ,
,![]()