题目内容
【题目】已知圆![]() ,直线
,直线![]() .
.

(1)求直线![]() 所过定点A的坐标;
所过定点A的坐标;
(2)求直线![]() 被圆C所截得的弦长最短时直线
被圆C所截得的弦长最短时直线![]() 的方程及最短弦长;
的方程及最短弦长;
(3)已知点M(-3,4),在直线MC上(C为圆心),存在定点N(异于点M),满足:对于圆C上任一点P,都有![]() 为一常数, 试求所有满足条件的点N的坐标及该常数.
为一常数, 试求所有满足条件的点N的坐标及该常数.
【答案】(1)A(1,3);(2)直线![]() 方程为
方程为![]() ,最短弦长为
,最短弦长为![]() ;(3)在直线MC上存在定点
;(3)在直线MC上存在定点![]() ,使得
,使得![]() 为常数
为常数![]() .
.
【解析】
(1)利用直线系方程的特征,直接求解直线![]() 过定点A的坐标;
过定点A的坐标;
(2)当AC⊥![]() 时,所截得弦长最短,由题知C(0,4),
时,所截得弦长最短,由题知C(0,4),![]() ,求出AC的斜率,利用点到直线的距离,转化求解即可;
,求出AC的斜率,利用点到直线的距离,转化求解即可;
(3)由题知,直线MC的方程为![]() ,假设存在定点N(
,假设存在定点N(![]() ,4)满足题意,则设
,4)满足题意,则设![]() ,
,![]() ,得
,得![]() ,且
,且![]() ,求出
,求出![]() ,然后求解比值.
,然后求解比值.
解:(1)依题意得,![]() ,
,
令![]() 且
且![]() ,得
,得![]() ,
,
∴直线![]() 过定点A(1,3);
过定点A(1,3);
(2)当AC⊥![]() 时,所截得弦长最短,由题知C(0,4),
时,所截得弦长最短,由题知C(0,4),![]() ,
,![]() ,得
,得![]() ,
,
∴由![]() 得
得![]() ,
,
此时直线![]() 方程为
方程为![]() ,
,
∴圆心到直线的距离为![]() ,
,
∴最短弦长为![]() ;
;
(3)由题知,直线MC的方程为![]() ,假设存在定点N(
,假设存在定点N(![]() ,4)满足题意,
,4)满足题意,
则设![]() ,
,![]() ,得
,得![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,
整理得,![]() ,
,
∵上式对任意![]() 恒成立,
恒成立,![]() 且
且![]() ,
,
解得 ![]() 或
或![]() (舍去,与M重合),
(舍去,与M重合),
综上可知,在直线MC上存在定点![]() ,使得
,使得![]() 为常数
为常数![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
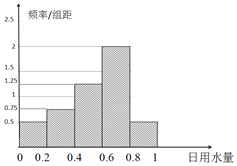
小学生10分钟应用题系列答案【题目】为达到节水节电的目的,某家庭记录了20天的日用电量xi(单位:度)的频数分布表和这20天相应的日用水量yi(单位:m3)的频率分布直方图如下:
日用电量xi | [0,2) | [2,4) | [4,6) | [6,8) | [8,10) |
频数(天) | 2 | 5 | 7 | 3 | 3 |
(1)假设水费为2.5元/m3,电费为0.6元/度,用以上数据估计该家庭日用电量的平均值和日用水量的平均值,并据此估计该家庭一个月的水费和电费一共是多少?(一个月按30天算,同一组中的数据以这组数据所在区间中点的值作代表);
(2)假设该家庭的日用水量y和日用电量x可用线性回归模型来拟合,请利用(1)中的计算数据及所给的参考数据和公式,建立y与x的回归方程,预测若该家庭日用电量为20度时的日用水量是多少m3?(回归方程的系数小数点后保留2位小数)
参考数据:![]() xiyi=65,
xiyi=65,![]() 612
612
参考公式:回归方程![]() x
x![]() 中斜率和截距的公式分别为:
中斜率和截距的公式分别为:
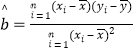 ,
,![]()
【题目】某市公交公司为了鼓励广大市民绿色出行,计划在某个地段增设一个起点站,为了研究车辆发车的间隔时间![]() 与乘客等候人数
与乘客等候人数![]() 之间的关系,经过抽样调查五个不同时段的情形,统计得到如下数据:
之间的关系,经过抽样调查五个不同时段的情形,统计得到如下数据:
间隔时间( | 8 | 10 | 12 | 14 | 16 |
等候人数( | 16 | 19 | 23 | 26 | 29 |
调查小组先从这5组数据中选取其中的4组数据求得线性回归方程,再用剩下的1组数据进行检验,检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值不超过1,则称所求的回归方程是“理想回归方程”.
的差,若差值的绝对值不超过1,则称所求的回归方程是“理想回归方程”.
(1)若选取的是前4组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判断所求方程是否是“理想回归方程”;
,并判断所求方程是否是“理想回归方程”;
(2)为了使等候的乘客不超过38人,试用所求方程估计间隔时间最多可以设为多少分钟?
参考公式:用最小二乘法求线性回归方程![]() 的系数公式:
的系数公式:
 ,
,![]() .
.



