题目内容
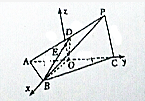 如图,在三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D是PA的中点,二面角P-AC-B为120°,PC=2,AB=2
如图,在三棱锥P-ABC中,△ABC是正三角形,∠PCA=90°,D是PA的中点,二面角P-AC-B为120°,PC=2,AB=2| 3 |
(1)求B、D、P三点的坐标;
(2)求BD与地面ABC所成角的余弦值.
考点:直线与平面所成的角,空间中的点的坐标
专题:空间角,坐标系和参数方程
分析:(1)首先利用建立的空间直角坐标系,即三角形的边角关系,二面角求出相关的线段长,进一步求出空间坐标.
(2)利用(1)的结论首先求出线面的夹角,进一步利用相关的运算求出结果.
(2)利用(1)的结论首先求出线面的夹角,进一步利用相关的运算求出结果.
解答:
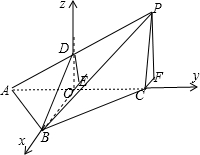 解:建立空间直角坐标系O-xyz,
解:建立空间直角坐标系O-xyz,
由于:△ABC是正三角形,AB=2
则:AO=OC=
,OB=3,
又∠PCA=90°,D是PA的中点,PC=2,
则:BD=1
二面角P-AC-B为120°,过D做DE⊥平面ABC,过P点做PF⊥平面ABC
得到DE=
,OE=
,PF=
,CF=1
所以求得B(-
,0,
),B(3,0,0),P(-1,
,
)
(2)利用(1)的结论:∠DBE是BD与地面ABC所成角.
利用余弦定理解得:BD=
,BE=
则:cos∠DBE=
=
所以:BD与地面ABC所成角的余弦值为:
 解:建立空间直角坐标系O-xyz,
解:建立空间直角坐标系O-xyz,由于:△ABC是正三角形,AB=2
| 3 |
则:AO=OC=
| 3 |
又∠PCA=90°,D是PA的中点,PC=2,
则:BD=1
二面角P-AC-B为120°,过D做DE⊥平面ABC,过P点做PF⊥平面ABC
得到DE=
| ||
| 2 |
| 1 |
| 2 |
| 3 |
所以求得B(-
| 1 |
| 2 |
| ||
| 2 |
| 3 |
| 3 |
(2)利用(1)的结论:∠DBE是BD与地面ABC所成角.
利用余弦定理解得:BD=
| ||
| 2 |
| 7 |
| 2 |
则:cos∠DBE=
| BE |
| BD |
7
| ||
| 13 |
所以:BD与地面ABC所成角的余弦值为:
7
| ||
| 13 |
点评:本题考查的知识要点:空间直角坐标系,线面的夹角,二面角的应用.属于基础题型.

练习册系列答案
相关题目
| 1+2sin500°cos500° |
| A、sin40°-cos40° |
| B、cos40°-sin40° |
| C、sin40°+cos40° |
| D、sin40°•cos40° |
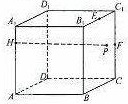 如图,已知正方体ABCD-A1B1C1D1的棱长为4,点H在棱AA1上,且HA1=1,点E、F分别为B1C1、CC1的中点,P为侧面BCC1B1上一动点,且PE⊥PF,则当点P运动时,求HP2的最小值是( )
如图,已知正方体ABCD-A1B1C1D1的棱长为4,点H在棱AA1上,且HA1=1,点E、F分别为B1C1、CC1的中点,P为侧面BCC1B1上一动点,且PE⊥PF,则当点P运动时,求HP2的最小值是( )| A、9 | ||
B、27--6
| ||
C、51-14
| ||
D、14-3
|
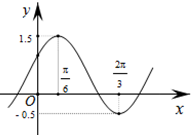 已知函数y=Asin(ωx+φ)+b的一部分图象如图所示,若A>0,ω>0,|φ|<
已知函数y=Asin(ωx+φ)+b的一部分图象如图所示,若A>0,ω>0,|φ|<