题目内容
已知函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)的图象关于y轴对称,其图象上相邻的两个最高点间的距离为2π,求f(x)的解析式.
考点:由y=Asin(ωx+φ)的部分图象确定其解析式
专题:三角函数的图像与性质
分析:由图象上相邻的两个最高点之间的距离为2π.可得周期,从而得到ω=1,再由函数f(x)为偶函数,得到φ=
,从而得到函数式.
| π |
| 2 |
解答:
解:由图象上相邻的两个最高点之间的距离为2π,
即有T=2π,ω=
=1,
由函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)的图象关于y轴对称,
则φ=kπ+
,k为整数,由0≤φ≤π,则φ=
,
则f(x)=sin(x+
)=cosx.
即有T=2π,ω=
| 2π |
| T |
由函数f(x)=sin(ωx+φ)(ω>0,0≤φ≤π)的图象关于y轴对称,
则φ=kπ+
| π |
| 2 |
| π |
| 2 |
则f(x)=sin(x+
| π |
| 2 |
点评:本题考查三角函数的图象和性质,考查三角恒等变换公式的运用,考查函数的奇偶性和周期性及运用,考查化简计算能力,属于基本知识的考查.

练习册系列答案
相关题目
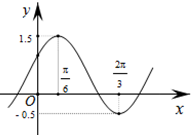 已知函数y=Asin(ωx+φ)+b的一部分图象如图所示,若A>0,ω>0,|φ|<
已知函数y=Asin(ωx+φ)+b的一部分图象如图所示,若A>0,ω>0,|φ|< 如图,E,F是边长为3的正方形ABCD的边AD上两个点,且AE=DF.连接CF交BD于G,连接BE交AG于点H,若|CH|2:|CE|2=9:10,则AE的长为
如图,E,F是边长为3的正方形ABCD的边AD上两个点,且AE=DF.连接CF交BD于G,连接BE交AG于点H,若|CH|2:|CE|2=9:10,则AE的长为