Question

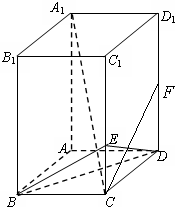如图所示，在长方体ABCD-A₁B₁C₁D₁中，AB=BC=2，BB₁=4，E是棱CC₁上的点，且CE=1；F是DD₁中点
（1）求异面直线DB与CF所成角的大小；
（2）求证：A₁C⊥平面BDE．
（3）求二面角B-DE-C的余弦值．

Answer 1

考点：二面角的平面角及求法,异面直线及其所成的角,直线与平面垂直的判定

专题：计算题,空间位置关系与距离,空间角

分析：以点A为原点，AB、AD、AA₁所在直线分别为x轴、y轴和z轴，建立空间直角坐标系，
（1）

DB

=（2，-2，0），

CF

=（-2，0，2），利用向量的夹角公式，即可求异面直线DB与CF所成角的大小；
（2）证明

A1C

•

DB

=2×2+2×(-2)+(-4)×0=0，

A1C

•

BE

=2×0+2×2+(-4)×1=0，即可证明A₁C⊥平面BDE．
（3））

A1C

=(2，2，-4)是平面BDE的一个法向量，

j

=(0，1，0)是平面CDE的一个法向量，向量

A1C

与

j

所成角是二面角B-DE-C的平面角（或其补角），利用向量的夹角公式求二面角B-DE-C的余弦值．

解答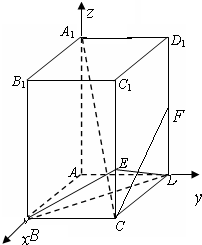： 解：以点A为原点，AB、AD、AA₁所在直线分别为x轴、y轴和z轴，建立空间直角坐标系，则B（2，0，0）、D（0，2，0）、C（2，2，0），E（2，2，1）、F（0，2，2），A₁（0，0，4）
（1）

DB

=（2，-2，0），

CF

=（-2，0，2），设异面直线DB与CF所成角为θ，则cosθ=

|-4|

2 2 ×2 2

=

1

2

，（5分）
∴θ=60°，即异面直线DB与CF所成角为60°  …（6分）
（2）∴

A1C

=(2，2，-4)，

BE

=(0，2，1)．        …（7分）
∵

A1C

•

DB

=2×2+2×(-2)+(-4)×0=0，

A1C

•

BE

=2×0+2×2+(-4)×1=0，
∴

A1C

⊥

BD

，

A1C

⊥

BE

．
∴A₁C⊥BE，A₁C⊥BD． …（9分）
∵BE∩BD=B，BE?平面BDE，ED?平面BDE，∴A₁C⊥平面BDE． …（10分）
（3）由（2）

A1C

=(2，2，-4)是平面BDE的一个法向量…（11分）

j

=(0，1，0)是平面CDE的一个法向量             …（12分）
向量

A1C

与

j

所成角是二面角B-DE-C的平面角（或其补角），
∴cos＜

A1C

，

j

＞=

A1C • j

|A1C| •| j|

=

6

6

∴二面角B-DE-C的余弦值为

6

6

…（14分）

点评：本题考查二面角的平面角及求法、考查异面直线及其所成的角、考查直线与平面垂直的判定，考查向量法的运用，属于中档题．