题目内容
【题目】如图1,在三棱锥P﹣ABC中,PA⊥平面ABC,AC⊥BC,D为侧棱PC上一点,它的正(主)视图和侧(左)视图如图2所示. 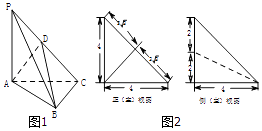
(1)证明:AD⊥BC;
(2)求三棱锥D﹣ABC的体积.
【答案】
(1)证明:因为PA⊥平面ABC,所以PA⊥BC,
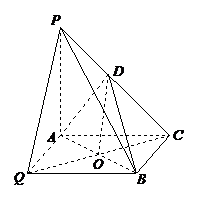
又AC⊥BC,所以BC⊥平面PAC,
所以BC⊥AD
由三视图可得,
在△PAC中,PA=AC=4,D为PC中点,
所以AD⊥PC,
所以AD⊥平面PBC
又因为BC面PBC,
故AD⊥BC
(2)解:由三视图可得BC=4,
由(1)知∠ADC=90°,BC⊥平面PAC
又三棱锥D﹣ABC的体积即为三棱锥B﹣ADC的体积,
所以,所求三棱锥的体积 ![]()
【解析】(1)先证明BC⊥平面PAC,再证明AD⊥平面PBC,进而可得AD⊥BC;(2)三棱锥D﹣ABC的体积即为三棱锥B﹣ADC的体积,进而得到答案.
【考点精析】认真审题,首先需要了解由三视图求面积、体积(求体积的关键是求出底面积和高;求全面积的关键是求出各个侧面的面积).

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目