题目内容
【题目】已知不等式组 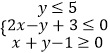 表示的平面区域为D,若(x,y)∈D,|x|+2y≤a为真命题,则实数a的取值范围是( )
表示的平面区域为D,若(x,y)∈D,|x|+2y≤a为真命题,则实数a的取值范围是( )
A.[10,+∞)
B.[11,+∞)
C.[13,+∞)
D.[14,+∞)
【答案】D
【解析】解:不等式组 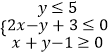 表示的平面区域为D,如图: 当x≥0时,z=|x|+2y=x+2y,z=x+2y经过B时取得最大值,
表示的平面区域为D,如图: 当x≥0时,z=|x|+2y=x+2y,z=x+2y经过B时取得最大值,
由 ![]() 可得B(1,5),此时z的最大值为:11.
可得B(1,5),此时z的最大值为:11.
当x<0时,z=|x|+2y=﹣x+2y,z=﹣x+2y经过A时取得最大值,
由 ![]() ,可得A(﹣4,5),此时z的最大值为:14.
,可得A(﹣4,5),此时z的最大值为:14.
若(x,y)∈D,|x|+2y≤a为真命题,则实数a的取值范围:[14,+∞).
故选:D.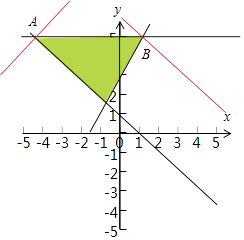
【考点精析】利用命题的真假判断与应用对题目进行判断即可得到答案,需要熟知两个命题互为逆否命题,它们有相同的真假性;两个命题为互逆命题或互否命题,它们的真假性没有关系.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =﹣20,
=﹣20, ![]() =
= ![]() ﹣
﹣ ![]()
![]()
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入﹣成本)