题目内容
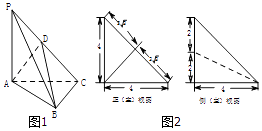
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是梯形,
是梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,侧面
,侧面![]() 底面
底面![]() .
.
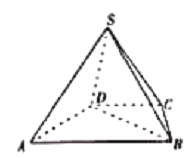
(1)求证:平面![]() 平面
平面![]() ;
;
(2)若![]() 与底面
与底面![]() 所成角为
所成角为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
【答案】(1)证明见解析;(2) ![]() .
.
【解析】试题分析:(1):取AB中点M,连接DM,可得DB⊥AD又侧面SAD⊥底面ABCD,可得BD⊥平面SAD,即可得平面SBD⊥平面SAD(2)以D为原点,DA,DB所在直线分别为x,y轴建立空间直角坐标系,求出设面SCB的法向量为: ![]() ,面SBD的法向量为
,面SBD的法向量为![]() .利用向量即可求解.
.利用向量即可求解.
解析:(1)因为![]() ,
, ![]() ,
,
所以![]() ,
, ![]() 是等腰直角三角形,
是等腰直角三角形,
故![]() ,
,
因为![]() ,
, ![]() ,
,
所以![]() ∽
∽![]() ,
,
![]() ,即
,即![]() ,
,
因为侧面![]() 底面
底面![]() ,交线为
,交线为![]() ,
,
所以![]() 平面
平面![]() ,所以平面
,所以平面![]() 平面
平面![]() .
.
(2)过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,
,
因为侧面![]() 底面
底面![]() ,
,
所以![]() 底面
底面![]() ,
,
所以![]() 是底面
是底面![]() 与底面
与底面![]() 所成的角,即
所成的角,即![]() ,
,
过点![]() 在平面
在平面![]() 内作
内作![]() ,
,
因为侧面![]() 底面
底面![]() ,
,
所以![]() 底面
底面![]() ,
,
如图建立空间直角坐标系![]() ,
,
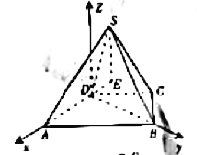
设![]() ,
, 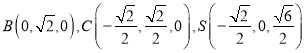 ,
,
则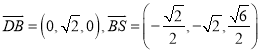 ,
, 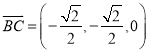 ,
,
设![]() 是平面
是平面![]() 法向量,
法向量,
则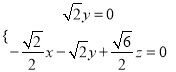
取![]() ,
,
设![]() 是平面
是平面![]() 的法向量,
的法向量,
则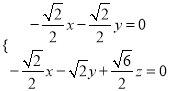
取![]() ,
, 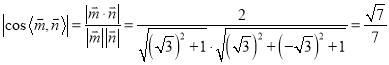
所以二面角![]() 的余弦值为
的余弦值为![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程 ![]() =
= ![]() x+
x+ ![]() ,其中
,其中 ![]() =﹣20,
=﹣20, ![]() =
= ![]() ﹣
﹣ ![]()
![]()
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入﹣成本)
【题目】某学校一个生物兴趣小组对学校的人工湖中养殖的某种鱼类进行观测研究,在饲料充足的前提下,兴趣小组对饲养时间x(单位:月)与这种鱼类的平均体重y(单位:千克)得到一组观测值,如下表:
xi(月) | 1 | 2 | 3 | 4 | 5 |
yi(千克) | 0.5 | 0.9 | 1.7 | 2.1 | 2.8 |

(1)在给出的坐标系中,画出关于x,y两个相关变量的散点图.
(2)请根据上表提供的数据,用最小二乘法求出变量y关于变量x的线性回归直线方程 ![]() .
.
(3)预测饲养满12个月时,这种鱼的平均体重(单位:千克)
(参考公式: ![]() =
=  ,
, ![]() )
)