题目内容
(本小题满分12分)已知点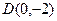 ,过点
,过点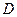 作抛物线
作抛物线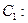
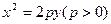 的切线
的切线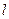 ,切点
,切点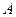 在第二象限,如图.
在第二象限,如图.
(Ⅰ)求切点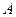 的纵坐标;
的纵坐标;
(Ⅱ)若离心率为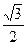 的椭圆
的椭圆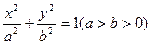 恰好经过切点
恰好经过切点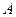 ,设切线
,设切线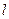 交椭圆的另一点为
交椭圆的另一点为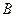 ,记切线
,记切线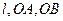 的斜率分别为
的斜率分别为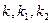 ,若
,若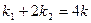 ,求椭圆方程.
,求椭圆方程.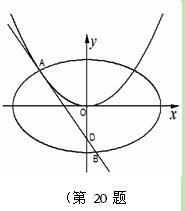
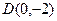 ,过点
,过点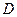 作抛物线
作抛物线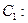
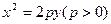 的切线
的切线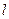 ,切点
,切点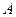 在第二象限,如图.
在第二象限,如图.(Ⅰ)求切点
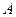 的纵坐标;
的纵坐标;(Ⅱ)若离心率为
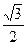 的椭圆
的椭圆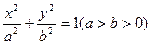 恰好经过切点
恰好经过切点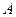 ,设切线
,设切线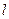 交椭圆的另一点为
交椭圆的另一点为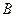 ,记切线
,记切线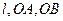 的斜率分别为
的斜率分别为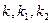 ,若
,若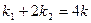 ,求椭圆方程.
,求椭圆方程.
解:(Ⅰ)设切点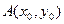 ,且
,且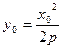
 ,
,
由切线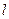 的斜率为
的斜率为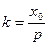 ,得
,得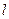 的方程为
的方程为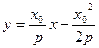 ,又点
,又点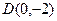 在
在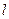 上,
上,
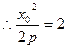 ,即点
,即点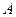 的纵坐标
的纵坐标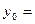
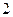 .
.
(Ⅱ)由(Ⅰ) 得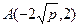 ,切线斜率
,切线斜率
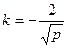 ,
,
设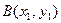 ,切线方程为
,切线方程为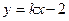 ,由
,由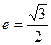 ,得
,得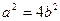 ,所以椭圆方程为
,所以椭圆方程为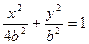 ,且过
,且过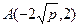 ,
,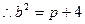
由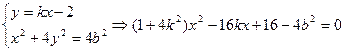 ,
,
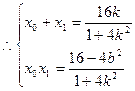 ,
,
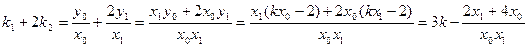
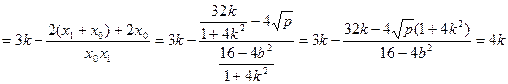
将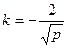 ,
,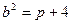 代入得:
代入得: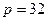 ,所以
,所以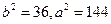 ,
,
椭圆方程为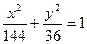 .
.
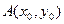 ,且
,且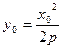
 ,
,由切线
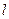 的斜率为
的斜率为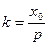 ,得
,得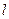 的方程为
的方程为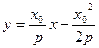 ,又点
,又点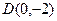 在
在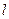 上,
上,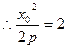 ,即点
,即点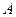 的纵坐标
的纵坐标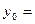
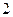 .
.(Ⅱ)由(Ⅰ) 得
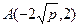 ,切线斜率
,切线斜率
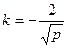 ,
,设
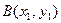 ,切线方程为
,切线方程为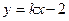 ,由
,由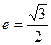 ,得
,得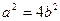 ,所以椭圆方程为
,所以椭圆方程为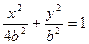 ,且过
,且过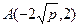 ,
,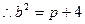
由
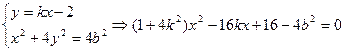 ,
,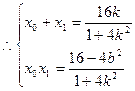 ,
,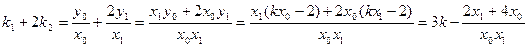
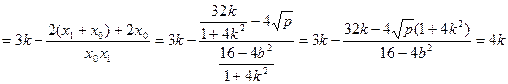
将
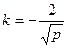 ,
,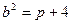 代入得:
代入得: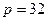 ,所以
,所以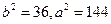 ,
,椭圆方程为
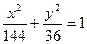 .
.略

练习册系列答案
相关题目
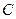 上的动点
上的动点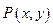 满足到点
满足到点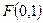 的距离比到直线
的距离比到直线 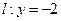 的距离小
的距离小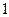 .
. 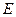 在直线
在直线 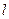 上,过点
上,过点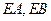 ,切点分别为
,切点分别为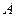 、
、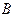 .
.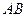 恒过一定点,并求出该定点的坐标;
恒过一定点,并求出该定点的坐标;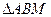 为等边三角形(
为等边三角形(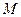 点也在直线
点也在直线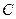 :
: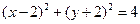 外一动点
外一动点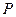 向圆
向圆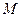 ,且
,且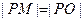 (
(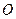 为坐标原点),求
为坐标原点),求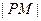 的最小值和
的最小值和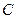 的中心在原点,焦点在
的中心在原点,焦点在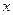 轴上,点
轴上,点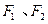 分别是椭圆的左、右焦点,在直线
分别是椭圆的左、右焦点,在直线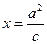 (
(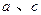 分别为椭圆的长半轴和半焦距的长)上的点
分别为椭圆的长半轴和半焦距的长)上的点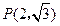 ,满足线段
,满足线段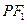 的中垂线过点
的中垂线过点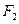 .过原点
.过原点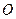 且斜率均存在的直线
且斜率均存在的直线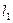 、
、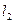 互相垂直,且截椭圆所得的弦长分别为
互相垂直,且截椭圆所得的弦长分别为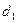 、
、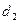 .
.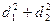 的最小值及取得最小值时直线
的最小值及取得最小值时直线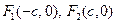 是椭圆
是椭圆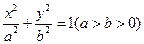 的左、右焦点,过点
的左、右焦点,过点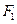 作
作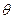 的动直线
的动直线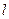 交椭圆于
交椭圆于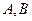 两点.当
两点.当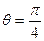 时,
时,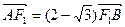 ,且
,且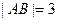 .
.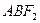 面积的最大值,并求出使面积达到最大值时直线
面积的最大值,并求出使面积达到最大值时直线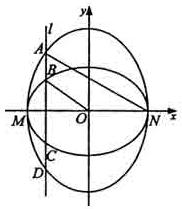
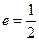 ,求
,求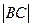 与
与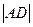 的比值;
的比值; 所表示的曲线为
所表示的曲线为 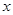 轴上的椭圆
轴上的椭圆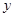 轴上的椭圆
轴上的椭圆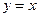 与抛物线C相交
与抛物线C相交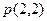 是AB的中点,则抛物线C的方程为_______________.
是AB的中点,则抛物线C的方程为_______________. 中,
中, 且
且 ,设
,设 ,以
,以 、
、 为焦点且过点
为焦点且过点 的双曲线的离心率为
的双曲线的离心率为 ,以
,以 、
、 ,则
,则 =__________
=__________