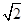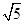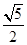题目内容
(本题满分10分)已知曲线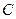 上的动点
上的动点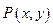 满足到点
满足到点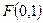 的距离比到直线
的距离比到直线 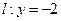 的距离小
的距离小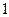 .
.
(1)求曲线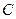 的方程;
的方程;
(2)动点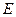 在直线
在直线 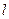 上,过点
上,过点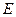 作曲线
作曲线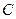 的切线
的切线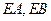 ,切点分别为
,切点分别为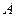 、
、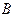 .
.
(ⅰ)求证:直线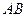 恒过一定点,并求出该定点的坐标;
恒过一定点,并求出该定点的坐标;
(ⅱ)在直线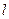 上是否存在一点
上是否存在一点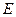 ,使得
,使得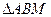 为等边三角形(
为等边三角形(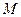 点也在直线
点也在直线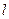 上)?若存在,求出点
上)?若存在,求出点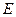 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
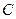 上的动点
上的动点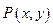 满足到点
满足到点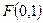 的距离比到直线
的距离比到直线 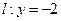 的距离小
的距离小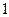 .
. (1)求曲线
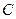 的方程;
的方程;(2)动点
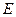 在直线
在直线 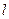 上,过点
上,过点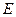 作曲线
作曲线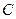 的切线
的切线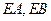 ,切点分别为
,切点分别为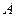 、
、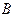 .
.(ⅰ)求证:直线
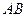 恒过一定点,并求出该定点的坐标;
恒过一定点,并求出该定点的坐标;(ⅱ)在直线
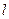 上是否存在一点
上是否存在一点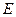 ,使得
,使得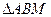 为等边三角形(
为等边三角形(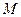 点也在直线
点也在直线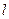 上)?若存在,求出点
上)?若存在,求出点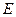 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由..解:(1) 曲线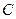 的方程
的方程 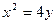 --------------3分
--------------3分
(2)(ⅰ)设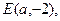
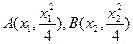 ,
,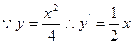
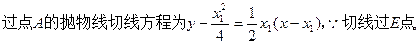
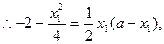 整理得:
整理得: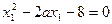
同理可得: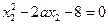

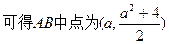
又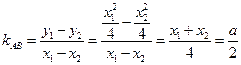

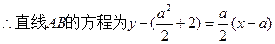
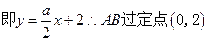 --------------------------6分
--------------------------6分
(ⅱ)由(ⅰ)知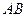 中点
中点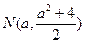 ,
,
当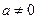 时,则
时,则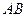 的中垂线方程为
的中垂线方程为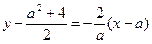
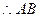 的中垂线与直线
的中垂线与直线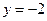 的交点
的交点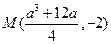
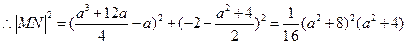
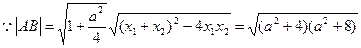
若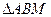 为等边三角形,则
为等边三角形,则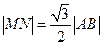
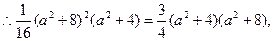
解得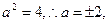 此时
此时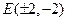 ,
,
当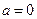 时,经检验不存在满足条件的点
时,经检验不存在满足条件的点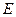
综上可得:满足条件的点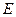 存在,坐标为
存在,坐标为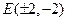 .----------------------10分
.----------------------10分
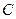 的方程
的方程 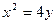 --------------3分
--------------3分(2)(ⅰ)设
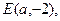
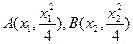 ,
,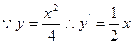
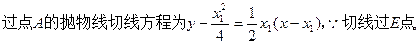
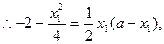 整理得:
整理得: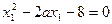
同理可得:
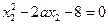

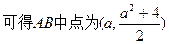
又
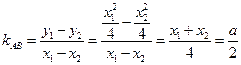

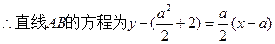
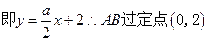 --------------------------6分
--------------------------6分(ⅱ)由(ⅰ)知
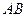 中点
中点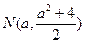 ,
,
当
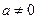 时,则
时,则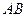 的中垂线方程为
的中垂线方程为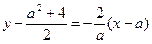
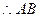 的中垂线与直线
的中垂线与直线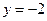 的交点
的交点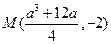
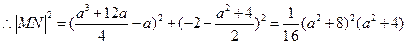
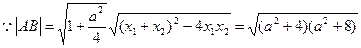
若
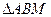 为等边三角形,则
为等边三角形,则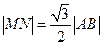
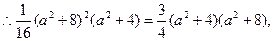
解得
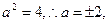 此时
此时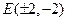 ,
,当
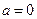 时,经检验不存在满足条件的点
时,经检验不存在满足条件的点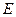
综上可得:满足条件的点
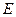 存在,坐标为
存在,坐标为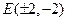 .----------------------10分
.----------------------10分略

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
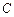 :
: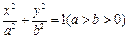 的离心率为
的离心率为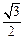 ,且过
,且过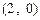 点.⑴求椭圆
点.⑴求椭圆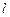 :
: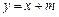 与椭圆
与椭圆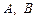 两点,
两点,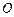 为坐标原点,若
为坐标原点,若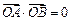 ,求
,求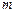 的值。
的值。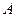 (1,0)和定圆B:
(1,0)和定圆B: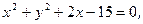 动圆P和定圆B相切并过A点,
动圆P和定圆B相切并过A点,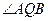 的最大值。
的最大值。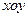 中,设点
中,设点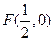 ,直线
,直线 :
: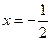 ,点
,点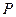 在直线
在直线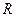 是线段
是线段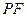 与
与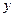 轴的交点,
轴的交点, 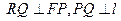 .
.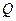 的轨迹的方程
的轨迹的方程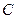 ;
; 过
过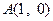 ,且圆心
,且圆心 线
线
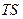 是圆
是圆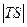 是否为定值?请说明理由.
是否为定值?请说明理由.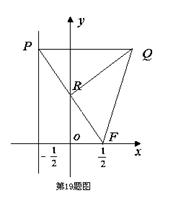
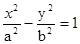 与椭圆
与椭圆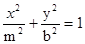 (a>0,m>b>0)的离心率互为倒数,那
(a>0,m>b>0)的离心率互为倒数,那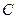 的顶点在原点,焦点F与双曲线
的顶点在原点,焦点F与双曲线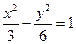 的右焦点重合,过点
的右焦点重合,过点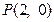 且斜率为1的直线
且斜率为1的直线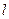 与抛物线
与抛物线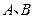 两点
两点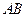 中点到抛物线准线的距离
中点到抛物线准线的距离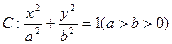 的左、右焦点分别为F1与
的左、右焦点分别为F1与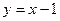 过椭圆的一个焦点F2且与椭圆交于P、Q两点,若
过椭圆的一个焦点F2且与椭圆交于P、Q两点,若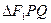 的周长为
的周长为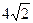 。
。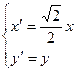 变成曲线
变成曲线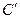 ,直线
,直线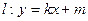 与曲线
与曲线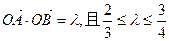 ,求
,求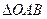 面积的取值范围。(O为坐标原点)
面积的取值范围。(O为坐标原点)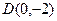 ,过点
,过点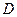 作抛物线
作抛物线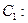
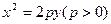 的切线
的切线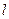 ,切点
,切点 在第二象限,如图.
在第二象限,如图.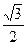 的椭圆
的椭圆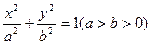 恰好经过切点
恰好经过切点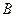 ,记切线
,记切线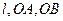 的斜率分别为
的斜率分别为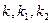 ,若
,若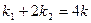 ,求椭圆方程.
,求椭圆方程.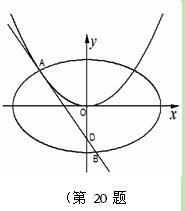
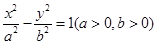 的一条渐近线方程为
的一条渐近线方程为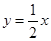 ,则该双曲线的离心率的值为
,则该双曲线的离心率的值为