题目内容
12.已知角α的终边上一点的坐标为(sin$\frac{3π}{4}$,cos$\frac{3π}{4}$),则角α的最小正值为$\frac{7π}{4}$.分析 根据角α的终边经过点M,且点M在第四象限,tanα═-1,从而求得角α的最小正值.
解答 解:角α的终边上一点的坐标为M(sin$\frac{3π}{4}$,cos$\frac{3π}{4}$),即 M($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$),故点M在第四象限,且tanα=$\frac{-\frac{\sqrt{2}}{2}}{\frac{\sqrt{2}}{2}}$=-1,
则角α的最小正值为$\frac{7π}{4}$,
故答案为:$\frac{7π}{4}$.
点评 本题主要考查任意角的三角函数的定义,属于基础题.

练习册系列答案
相关题目
2.已知函数$f(x)=a(x-\frac{1}{x})-2lnx(a∈R)$,g(x)=-$\frac{a}{x}$,若至少存在一个x0∈[1,e],使得f(x0)>g(x0)成立,则实数a的取值范围为( )
| A. | [0,+∞) | B. | (0,+∞) | C. | [1,+∞) | D. | (1,+∞) |
3.定义在闭区间[a,b]上的连续函数y=f(x)有唯一的极值点x=x0,且y极小值=f(x0),则下列说法正确的是( )
| A. | 函数f(x)在[a,b]上不一定有最小值 | |
| B. | 函数f(x)在[a,b]上有最小值,但不一定是f(x0) | |
| C. | 函数f(x)在[a,b]上有最小值f(x0) | |
| D. | 函数f(x)在[a,b]上的最大值也可能是f(x0) |
7.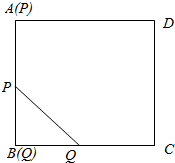 如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )
如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )
 如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )
如图,正方形ABCD的边长为1,点P从顶点A沿着A→B的方向向顶点B运动,速度为2,同时,点Q从顶点B沿着B→C方向向顶点C运动,速度为1,则|PQ|的最小值为( )| A. | 0 | B. | $\frac{\sqrt{5}}{5}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1 |
4.设$\overrightarrow{a}$=(x,2y,3),$\overrightarrow{b}$=(1,1,6),且$\overrightarrow{a}$∥$\overrightarrow{b}$,则x+y等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{2}$ | D. | 2 |