题目内容
1.已知0°<α<90°,0°<α+β<90°,3sinβ=sin(2α+β),则tanβ的最大值是$\frac{\sqrt{2}}{4}$.分析 由题意可得tanα>0,由和差角的公式和已知式子可得tan(α+β)=2tanα,可得tanβ=$\frac{tanα}{1+2ta{n}^{2}α}$=$\frac{1}{\frac{1}{tanα}+2tanα}$,由基本不等式可得最值.
解答 解:∵0°<α<90°,∴tanα>0
又∵3sinβ=sin(2α+β),
∴3sin[(α+β)-α]=sin[(α+β)+α],
∴3sin(α+β)cosα-3cos(α+β)sinα=sin(α+β)cosα+cos(α+β)sinα,
∴2sin(α+β)cosα=4cos(α+β)sinα,
∴tan(α+β)=2tanα,
∴tanβ=tan(α+β-α)=$\frac{tan(α+β)-tanα}{1+tan(α+β)tanα}$
=$\frac{tanα}{1+2ta{n}^{2}α}$=$\frac{1}{\frac{1}{tanα}+2tanα}$≤$\frac{1}{2\sqrt{\frac{1}{tanα}•2tanα}}$=$\frac{\sqrt{2}}{4}$,
当且仅当$\frac{1}{tanα}$=2tanα即tanα=$\frac{\sqrt{2}}{2}$时,上式取最大值$\frac{\sqrt{2}}{4}$,
故答案为:$\frac{\sqrt{2}}{4}$.
点评 本题考查两角和与差的三角函数公式,涉及基本不等式求最值,属中档题.

练习册系列答案
相关题目
11.若函数f(x)=x3-mx2-x+5在区间(0,1)内单调递减,则实数m的取值范围是( )
| A. | m≥1 | B. | m=1 | C. | m≤1 | D. | 0<m<1 |
6.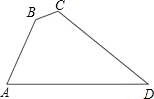 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )
 如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )
如图,在四边形ABCD中,∠B=135°,∠C=120°,AB=2$\sqrt{3}$,BC=4-2$\sqrt{2}$,CD=4$\sqrt{2}$,则AD边的长为( )| A. | 2$\sqrt{6}$ | B. | 4$\sqrt{6}$ | C. | 4+$\sqrt{6}$ | D. | 2+2$\sqrt{6}$ |