题目内容
2.设y=f(x)是二次函数,方程f(x)=0有两个相等的实根,且f′(x)=2x-2.(1)求y=f(x)的表达式;
(2)求y=f(x)的图象与两坐标轴所围成封闭图形的面积.
分析 (1)根据导函数的解析式设出原函数的解析式,根据有两个相等的实根可得答案.
(2)根据定积分的定义可得答案.
解答 解:(1)设f(x)=ax2+bx+c,则f′(x)=2ax+b,
又已知f′(x)=2x-2
∴a=1,b=-2.
∴f(x)=x2-2x+c
又方程f(x)=0有两个相等实根,
∴判别式△=4-4c=0,即c=1.
故f(x)=x2-2x+1.
(2)依题意,有所求面积=${∫}_{0}^{1}({x}^{2}-2x+1)dx=(\frac{1}{3}{x}^{3}-{x}^{2}+x){|}_{0}^{1}$=$\frac{1}{3}$
故y=f(x)的图象与两坐标轴所围成封闭图形的面积为$\frac{1}{3}$.
点评 本题主要考查导数的逆运算和定积分在求面积中的应用.属基础题.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
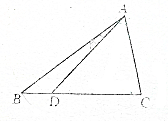 如图,在直角三角形ABC中,∠C=90°,D为BC边上的一点,且BC=4BD,设∠CAD=α,∠BAD=β,若tanα=7tanβ,求角α的大小.
如图,在直角三角形ABC中,∠C=90°,D为BC边上的一点,且BC=4BD,设∠CAD=α,∠BAD=β,若tanα=7tanβ,求角α的大小.