题目内容
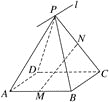
【题目】如图所示,正方体ABCD﹣A′B′C′D′的棱长为1,E、F分别是棱是AA′,CC′的中点,过直线EF的平面分别与棱BB′,DD′交于M,N,设BM=x,x∈[0,1],给出以下四种说法:

(1)平面MENF⊥平面BDD′B′;
(2)当且仅当x=![]() 时,四边形MENF的面积最小;
时,四边形MENF的面积最小;
(3)四边形MENF周长L=f(x),x∈[0,1]是单调函数;
(4)四棱锥C′﹣MENF的体积V=h(x)为常函数,以上说法中正确的为( )
A. (2)(3) B. (1)(3)(4) C. (1)(2)(4) D. (1)(2)
【答案】C
【解析】
(1)利用面面垂直的判定定理去证明EF⊥平面BDD′B′;(2)四边形MENF的对角线EF是固定的,所以要使面积最小,则只需MN的长度最小即可;(3)判断周长的变化情况;(4)求出四棱锥的体积,进行判断.
(1)连结BD,B′D′,则由正方体的性质可知,EF⊥平面BDD′B′,所以平面MENF⊥平面BDD′B′,所以正确;
(2)连结MN,因为EF⊥平面BDD′B′,所以EF⊥MN,四边形MENF的对角线EF是固定的,所以要使面积最小,则只需MN的长度最小即可,此时当M为棱的中点时,即x![]() 时,此时MN长度最小,对应四边形MENF的面积最小.所以正确;
时,此时MN长度最小,对应四边形MENF的面积最小.所以正确;
(3)因为EF⊥MN,所以四边形MENF是菱形.当x∈[0,![]() ]时,EM的长度由大变小.当x∈[
]时,EM的长度由大变小.当x∈[![]() ,1]时,EM的长度由小变大.所以函数L=f(x)不单调.所以错误;
,1]时,EM的长度由小变大.所以函数L=f(x)不单调.所以错误;
(4)连结C′E,C′M,C′N,则四棱锥则分割为两个小三棱锥,它们以C′EF为底,以M,N分别为顶点的两个小棱锥.因为三角形C′EF的面积是个常数.M,N到平面C'EF的距离是个常数,所以四棱锥C'﹣MENF的体积V=h(x)为常函数,所以正确.
故选:C.

【题目】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:
单价x(元) | 8 | 8.2 | 8.4 | 8.6 | 8.8 | 9 |
销量y(件) | 90 | 84 | 83 | 80 | 75 | 68 |
(1)求回归直线方程![]() =bx+a,其中b=-20,a=
=bx+a,其中b=-20,a=![]() -b
-b![]()
(2)预计在今后的销售中,销量与单价仍然服从(1)中的关系,且该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入—成本)