Question

【题目】如图，AB是圆O的直径，弦CD⊥AB于点M，点E是CD延长线上一点，AB=10，CD=8，3ED=4OM，EF切圆O于F，BF交CD于点G．

（1）求证：EF=EG；
（2）求线段MG的长．

Answer 1

【答案】
（1）证明：连接AF，OF，则A，F，G，M共圆，

∴∠FGE=∠BAF，

∵EF⊥OF，

∴∠EFG=∠FGE，

∴EF=EG

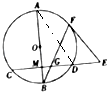
（2）解：由AB=10，CD=8可得OM=3，

∴ED= OM=4，EF2=EDEC=48，EF=EG=4 ，

连接AD，则∠BAD=∠BFD，

∴MG=EM﹣EG═8﹣4 ．

【解析】（1）由EF为圆的切线得∠EFG=∠BAF，由垂直关系可知点A、M、G、F四点共圆，从而得∠FGE=∠BAF，所以∠EFG=∠FGE（2）由已知及切线长定理可得，EF=EG=4 ，从而MG=EM﹣EG=8﹣4 ．