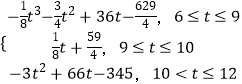题目内容
【题目】已知函数![]() 为奇函数,
为奇函数, ![]() 为常数.
为常数.
(1)确定![]() 的值;
的值;
(2)求证: ![]() 是
是![]() 上的增函数;
上的增函数;
(3)若对于区间![]() 上的每一个
上的每一个![]() 值,不等式
值,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
【答案】(1) ![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3) ![]() .
.
【解析】试题分析:
(1)由![]() 是奇函数可得
是奇函数可得![]() ,从而
,从而![]() ,整理得
,整理得![]() ,比较系数得
,比较系数得![]() ,验证得
,验证得![]() 不合题意,故
不合题意,故![]() 。(2)设
。(2)设![]() ,做差比较可得
,做差比较可得![]() ,故
,故![]() ,即
,即![]() ,证得结论成立。(3)分离参数得
,证得结论成立。(3)分离参数得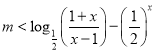 在
在![]() 上恒成立,设
上恒成立,设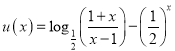 ,根据单调性求得
,根据单调性求得![]() ,从而可得结论。
,从而可得结论。
试题解析:
(1)∵函数![]() 是奇函数,
是奇函数,
![]() ,
,
即 ![]()
∴![]() ,
,
整理得![]() ,
,
∴![]() ,
,
解得![]() ,
,
当![]() 时,
时, ![]() ,不合题意舍去,
,不合题意舍去,
∴![]() 。
。
(2)由(1)可得![]() ,
,
设![]() ,
,
则![]() ,
,
∵![]() ,
,
∴![]()
∴![]() ,
,
∴![]() ,
,
∴![]() ,即
,即![]() .
.
∴![]() 是
是![]() 上的增函数.
上的增函数.
(3)依题意得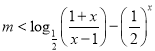 在
在![]() 上恒成立,
上恒成立,
设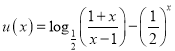 ,
, ![]() ,
,
由(2)知函数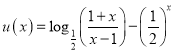 在
在![]() 上单调递增,
上单调递增,
∴当![]() ,
,
所以![]() .
.
故实数![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
相关题目
【题目】某厂商为了解用户对其产品是否满意,在使用产品的用户中随机调查了80人,结果如下表:
(1)根据上述,现用分层抽样的方法抽取对产品满意的用户5人,在这5人中任选2人,求被选中的恰好是男、女用户各1人的概率;
(2)有多大把握认为用户对该产品是否满意与用户性别有关?请说明理由.
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
注: ![]()