Question

【题目】如图所示，为平行四边形ABCD所在平面外一点，M,N分别为AB,PC的中点，平面PAD平面PBC＝.

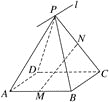
(1)求证：BC∥；

(2)MN与平面PAD是否平行？试证明你的结论．

Answer 1

【答案】（1）见解析；（2）见解析

【解析】

试题证明线线平行的方法；1，向量法，2.垂直于同一平面的两条直线平行，3平行于同一直线的两条直线平行，4一个平面与另外两个平行平面相交,那么两条交线也平行。线面平行，1平面外的一条直线与平面内的一条直线平行，则这条直线与这个平面平行，2若一条直线与一个平面同时平行于另一个平面且这条直线不属于这个平面，则这条直线与这个平面平行，3若一条直线与两平行平面中的一个平行，则这条直线与另一个平面平行，4，最好用的还是向量法。

试题解析：(1)证明 因为BC∥AD，AD平面PAD，

BC平面PAD，所以BC∥平面PAD.

又平面PAD∩平面PBC＝l，BC平面PBC，所以BC∥l.

(2)解 MN∥平面PAD.证明如下：

如图所示，取PD中点E，连结AE，EN.

又∵N为PC的中点，∴

又∵

∴

即四边形AMNE为平行四边形．

∴AE∥MN，又MN平面PAD，AE平面PAD

.∴MN∥平面PAD.