Question

【题目】已知等差数列{an}的前n项和为Sn ， a1=a．当n≥2时，Sn2=3n2an+Sn﹣12 ， an≠0，n∈N* ．
（1）求a的值；
（2）设数列{cn}的前n项和为Tn ， 且cn=3n﹣1+a5 ， 求使不等式4Tn＞Sn成立的最小正整数n的值．

Answer 1

【答案】
（1）解：∵a1=a，当n≥2时Sn2=3n2an+Sn﹣12，

∴（a+a2）2=12a2+a2， =27a3﹣（a+a2）2，

∵an≠0，

∴a2=12﹣2a，a3=3+2a，

∵a1+a3=2a2，

∴2（12﹣2a）=a+3+2a，解得a=3，

经检验，当a=3时an=3n，Sn= 、Sn﹣1= 满足Sn2=3n2an+Sn﹣12

（2）解：由（1）可知cn=3n﹣1+15，

∴Tn= +15n，

∵4Tn＞Sn，

∴4（ +15n）＞ ，

整理得：23n+60n﹣2＞165，即23n+60n＞167，

∵f（n）=23n+60n为增函数，且f（2）＜167、f（3）＞167，

∴满足条件的n的最小值为3．

【解析】（1）通过在Sn2=3n2an+Sn﹣12中令n=2、3，结合a1=a计算可知a2=12﹣2a、a3=3+2a，利用a1+a3=2a2计算可知a=3，验证其是否成立即可；（2）通过（1）可知cn=3n﹣1+15，进而利用分组求和法计算可知Tn= +15n，问题转化为解不等式4（ +15n）＞ ，计算即得结论．
【考点精析】本题主要考查了数列的前n项和的相关知识点，需要掌握数列{an}的前n项和sn与通项an的关系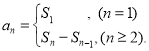才能正确解答此题．