题目内容
已知数列{an}的前n项和Sn=
(n∈N*,k是与n无关的正整数).
(1)求数列{an}的通项公式,并证明数列{an}是等差数列;
(2)设数列{an}满足不等式:|a1-1|+|a2-1|+…|a2k-1-1|+|a2k-1|≤6,求所有这样的k的值.
| n+n2 |
| 2k-1 |
(1)求数列{an}的通项公式,并证明数列{an}是等差数列;
(2)设数列{an}满足不等式:|a1-1|+|a2-1|+…|a2k-1-1|+|a2k-1|≤6,求所有这样的k的值.
(1)∵Sn=
(k是与n无关的正整数),
∴a1=
,
当n≥2时,an=Sn-Sn-1=
[(n2+n)-((n-1)2+(n-1))]=
,
当n=1时,a1=
也适合上式,
∴an=
.
∴an+1-an=
[2(n+1)-2n]=
为定值,
∴数列{an}是等差数列;
(2)∵an=
,
∴ak=
=1+
,
∴ak-1=
,
又数列{an}的公差d=
>0,故数列{an}为递增数列,
∴ak+1-1>
,
ak+2-1>
,…,
ak+k-1>
,
∴|ak-1|+|ak+1-1|+…+|ak+k-1|=ak-
+ak+1-+
…+ak+k-
>k+1,
∴
+
•
>k+1+
,
要使|a1-1|+|a2-1|+…|a2k-1-1|+|a2k-1|≤6,
需k+1<5(k∈N*),即1≤k≤4(k∈N*),
①当k=1时,a1=
=2,d=
=2,
∴an=2+(n-1)×2=2n,
∴|a1-1|+|a2-1|+…|a2k-1-1|+|a2k-1|=|a1-1|+|a2-1|=|2-1|+|4-1|=4≤6,即k=1时符合题意;
②当k=2时,a1=
=
,d=
=
,
同理可求an=
,
∴|a1-1|+|a2-1|+…|a2k-1-1|+|a2k-1|=|a1-1|+|a2-1|+…+|a4-1|=(1-
)+(
-1)+(2-1)+(
-1)=
<6,故k=2时符合题意;
③当k=3时,同理可求an=
n,
|a1-1|+|a2-1|+…+|a6-1|=
+(1-
)+(
-1)+(
-1)+(2-1)+(
-1)=4<6,故k=3时符合题意;
④当k=4时,同理可求an=
n,
|a1-1|+|a2-1|+…+|a8-1|=
+
+
+
+(
-1)+(
-1)+(
-1)+(
-1)=
<6.故k=4时符合题意;
综上所述,存在k=1,2,3,4使|a1-1|+|a2-1|+…|a2k-1-1|+|a2k-1|≤6成立.
| n+n2 |
| 2k-1 |
∴a1=
| 2 |
| 2k-1 |
当n≥2时,an=Sn-Sn-1=
| 1 |
| 2k-1 |
| 2n |
| 2k-1 |
当n=1时,a1=
| 2 |
| 2k-1 |
∴an=
| 2n |
| 2k-1 |
∴an+1-an=
| 1 |
| 2k-1 |
| 2 |
| 2k-1 |
∴数列{an}是等差数列;
(2)∵an=
| 2n |
| 2k-1 |
∴ak=
| 2k |
| 2k-1 |
| 1 |
| 2k-1 |
∴ak-1=
| 1 |
| 2k-1 |
又数列{an}的公差d=
| 2 |
| 2k-1 |
∴ak+1-1>
| 1 |
| 2k-1 |
ak+2-1>
| 1 |
| 2k-1 |
ak+k-1>
| 1 |
| 2k-1 |
∴|ak-1|+|ak+1-1|+…+|ak+k-1|=ak-
| 1 |
| 2k-1 |
| 1 |
| 2k-1 |
| 1 |
| 2k-1 |
∴
| (k+1)×2k |
| 2k-1 |
| (k+1)•k |
| 2 |
| 2 |
| 2k-1 |
| k+1 |
| 2k-1 |
要使|a1-1|+|a2-1|+…|a2k-1-1|+|a2k-1|≤6,
需k+1<5(k∈N*),即1≤k≤4(k∈N*),
①当k=1时,a1=
| 2 |
| 2k-1 |
| 2 |
| 2k-1 |
∴an=2+(n-1)×2=2n,
∴|a1-1|+|a2-1|+…|a2k-1-1|+|a2k-1|=|a1-1|+|a2-1|=|2-1|+|4-1|=4≤6,即k=1时符合题意;
②当k=2时,a1=
| 2 |
| 2k-1 |
| 2 |
| 3 |
| 2 |
| 2k-1 |
| 2 |
| 3 |
同理可求an=
| 2n |
| 3 |
∴|a1-1|+|a2-1|+…|a2k-1-1|+|a2k-1|=|a1-1|+|a2-1|+…+|a4-1|=(1-
| 2 |
| 3 |
| 4 |
| 3 |
| 8 |
| 3 |
| 10 |
| 3 |
③当k=3时,同理可求an=
| 2 |
| 5 |
|a1-1|+|a2-1|+…+|a6-1|=
| 3 |
| 5 |
| 4 |
| 5 |
| 6 |
| 5 |
| 8 |
| 5 |
| 12 |
| 5 |
④当k=4时,同理可求an=
| 2 |
| 7 |
|a1-1|+|a2-1|+…+|a8-1|=
| 5 |
| 7 |
| 3 |
| 7 |
| 1 |
| 7 |
| 1 |
| 7 |
| 10 |
| 7 |
| 12 |
| 7 |
| 14 |
| 7 |
| 16 |
| 7 |
| 34 |
| 7 |
综上所述,存在k=1,2,3,4使|a1-1|+|a2-1|+…|a2k-1-1|+|a2k-1|≤6成立.

练习册系列答案
相关题目
 满足:
满足: .
. 是等比数列;
是等比数列; ,且对任意的正整数
,且对任意的正整数 ,都有
,都有 ,求实数
,求实数 的取值范围.
的取值范围.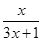 ,对于数列{an}有an=f(an-1)(n∈N*,且n≥2),如果a1=1,那么a2=________.an=________.
,对于数列{an}有an=f(an-1)(n∈N*,且n≥2),如果a1=1,那么a2=________.an=________.