题目内容
17.设点M(x,y)到直线x=4的距离与它到定点(1,0)的距离之比为2,并记点M的轨迹曲线为C.(Ⅰ)求曲线C的方程;
(Ⅱ)设过定点(0,2)的直线l与曲线C交于不同两点E、F,且∠EOF=90°,(其中O为坐标原点),求直线l的斜率k的值.
(Ⅲ)设A,B分别是曲线C的与X轴正半轴和Y轴正半轴的两个交点,直线y=mx(m>0)与曲线C交于P、Q两点,求四边形APBQ面积的最大值.
分析 (Ⅰ)利用点到直线、两点间的距离公式计算即得结论;
(Ⅱ)通过设直线l的方程:y=kx+2并与椭圆方程联立,利用∠EOF=90°即$\overrightarrow{OE}$$•\overrightarrow{OF}$=0、结合韦达定理及向量数量积的坐标运算,计算即得结论;
(Ⅲ)通过联立直线与椭圆方程可知P($\sqrt{\frac{12}{3+4{m}^{2}}}$,m•$\sqrt{\frac{12}{3+4{m}^{2}}}$)、Q(-$\sqrt{\frac{12}{3+4{m}^{2}}}$,-m•$\sqrt{\frac{12}{3+4{m}^{2}}}$),利用S四边形APBQ=2S△BOP+2S△QOA及基本不等式计算即得结论.
解答 解:(Ⅰ)∵点M(x,y)到直线x=4的距离与它到定点(1,0)的距离之比为2,
∴$\frac{|x-4|}{\sqrt{(x-1)^{2}+{y}^{2}}}$=2,
化简得:$\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1$;
(Ⅱ)由题意可设直线l的方程为:y=kx+2,
联立$\left\{\begin{array}{l}{y=kx+2}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,消去y整理得:(3+4k2)x2+16kx+4=0,
又∵直线l与曲线C交于不同两点E(x1,y1),F(x2,y2),
则△=(16k)2-4•4•(3+4k2)>0,解得:k<-$\frac{1}{2}$或k>$\frac{1}{2}$,
由韦达定理可知:x1+x2=-$\frac{16k}{3+4{k}^{2}}$,x1x2=$\frac{4}{3+4{k}^{2}}$,
∵∠EOF=90°,
∴$\overrightarrow{OE}$$•\overrightarrow{OF}$=0,即x1x2+y1y2=0,
∴x1x2+(kx1+2)(kx2+2)=0,
∴(1+k2)x1x2+2k(x1+x2)+4=0,
∴(1+k2)•$\frac{4}{3+4{k}^{2}}$-2k•$\frac{16k}{3+4{k}^{2}}$+4=0,
解得:k=±$\frac{2\sqrt{3}}{3}$,
显然k=±$\frac{2\sqrt{3}}{3}$∈(-∞,-$\frac{1}{2}$)∪($\frac{1}{2}$,+∞),
∴k=±$\frac{2\sqrt{3}}{3}$;
(Ⅲ)联立$\left\{\begin{array}{l}{y=mx(m>0)}\\{\frac{{x}^{2}}{4}+\frac{{y}^{2}}{3}=1}\end{array}\right.$,
解方程组得:$\left\{\begin{array}{l}{{x}_{1}=\sqrt{\frac{12}{3+4{m}^{2}}}}\\{{y}_{1}=m•\sqrt{\frac{12}{3+4{m}^{2}}}}\end{array}\right.$,$\left\{\begin{array}{l}{{x}_{2}=-\sqrt{\frac{12}{3+4{m}^{2}}}}\\{{y}_{2}=-m•\sqrt{\frac{12}{3+4{m}^{2}}}}\end{array}\right.$,
即P($\sqrt{\frac{12}{3+4{m}^{2}}}$,m•$\sqrt{\frac{12}{3+4{m}^{2}}}$),Q(-$\sqrt{\frac{12}{3+4{m}^{2}}}$,-m•$\sqrt{\frac{12}{3+4{m}^{2}}}$),
∴S四边形APBQ=2S△BOP+2S△QOA
=$2•\frac{1}{2}•$|BO|•xP+$2•\frac{1}{2}•$|OA|•yP
=$\sqrt{3}$•xP+2•yP
=$\sqrt{3}$•$\sqrt{\frac{12}{3+4{m}^{2}}}$+2•m•$\sqrt{\frac{12}{3+4{m}^{2}}}$
=($\sqrt{3}$+2m)•$\sqrt{\frac{12}{3+4{m}^{2}}}$
=2•$\sqrt{\frac{3(\sqrt{3}+2m)^{2}}{3+4{m}^{2}}}$
=2•$\sqrt{3(1+\frac{4\sqrt{3}m}{3+4{m}^{2}})}$
=$2\sqrt{3}$•$\sqrt{1+\frac{4\sqrt{3}}{4m+\frac{3}{m}}}$,
∵4m+$\frac{3}{m}$≥2$\sqrt{4m•\frac{3}{m}}$=4$\sqrt{3}$,当且仅当4m=$\frac{3}{m}$即m=$\frac{\sqrt{3}}{2}$时等号成立,
∴$2\sqrt{3}$•$\sqrt{1+\frac{4\sqrt{3}}{4m+\frac{3}{m}}}$≤$2\sqrt{3}$•$\sqrt{1+\frac{4\sqrt{3}}{4\sqrt{3}}}$=2$\sqrt{6}$,
∴当m=$\frac{\sqrt{3}}{2}$时,S四边形APBQ的最大面积为$2\sqrt{6}$.
点评 本题是一道直线与圆锥曲线的综合题,考查运算求解能力,注意解题方法的积累,属于中档题.

 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案| A. | $\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
| A. | $\left.\begin{array}{l}{a∥b}\\{b⊥α}\end{array}\right\}$⇒a⊥α | B. | $\left.\begin{array}{l}{a∥b}\\{b?α}\end{array}\right\}$⇒a∥α | C. | $\left.\begin{array}{l}{a⊥b}\\{b∥α}\end{array}\right\}$⇒a⊥α | D. | $\left.\begin{array}{l}{a⊥α}\\{a⊥b}\end{array}\right\}$⇒b?α |
| X | 5 | 6 | 7 | 8 |
| p | 0.4 | a | b | 0.1 |
| A. | a=0.3,b=0.2 | B. | a=0.2,b=0.3 | C. | a=0.4,b=0.1 | D. | a=0.1,b=0.4 |
 在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )
在某海滨小城打的士收费办法如下:不超过3公里收8元,超过3公里的里程每公里收2.6元,另每车次超过3公里收燃油附加费1元(其他因素不考虑).相应x>3收费系统的流程图如图所示,则①处应填( )| A. | y=8+2.6x | B. | y=9+2.6x | C. | y=8+2.6(x-3) | D. | y=9+2.6(x-3) |
(1)根据表中的数据,能否在犯错的概率不超过0.05的前提下认为视力与学习成绩有关系?
(2)根据表中数据,在调查的100名学生中,按照分层抽样在不近视的学生中抽取了9人,进一步调查他们良好的护眼习惯,并且在这9人中任取3人,记名次在1~50名的学生人数为X,求X的分布列和数学期望.
| 年级名次 是否近视 | 1~50 | 951~1000 |
| 近视 | 41 | 32 |
| 不近视 | 9 | 18 |
| A. | $\frac{{3\sqrt{3}+4}}{10}$ | B. | $\frac{{3\sqrt{3}-4}}{10}$ | C. | $\frac{{4-3\sqrt{3}}}{10}$ | D. | $-\frac{{3\sqrt{3}+4}}{10}$ |
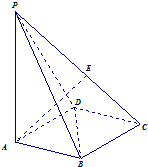 如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.
如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.