题目内容
2．
在某海滨小城打的士收费办法如下：不超过3公里收8元，超过3公里的里程每公里收2.6元，另每车次超过3公里收燃油附加费1元（其他因素不考虑）．相应x＞3收费系统的流程图如图所示，则①处应填（ ）| A． | y=8+2.6x | B． | y=9+2.6x | C． | y=8+2.6（x-3） | D． | y=9+2.6（x-3） |
分析 由题意可得：当满足条件x＞3时，即里程超过3公里，应按超过3公里的里程每公里收2.6元，另每车次超过3公里收燃油附加费1元收费，进而可得函数的解析式．
解答 解：当满足条件x＞3时，即里程超过3公里，
超过3公里时，每车收燃油附加费1元，并且超过的里程每公里收2.6元
∴y=2.6（x-3）+8+1=9+2.6（x-3），
故选：D．
点评 程序填空是重要的考试题型，这种题考试的重点有：①分支的条件②循环的条件③变量的赋值④变量的输出．此种题型的易忽略点是：不能准确理解流程图的含义而导致错误，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
12．在△ABC中，若∠B=30°，AB=2$\sqrt{3}$，AC=2，则△ABC的面积为（ ）
| A． | $\sqrt{3}$ | B． | 2$\sqrt{3}$或$\sqrt{2}$ | C． | 2$\sqrt{3}$或$\sqrt{3}$ | D． | 2$\sqrt{3}$ |
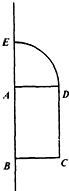如图所示，矩形ABCD和一个圆心角为90°的扇形拼在一起，其中AB=2，BC=AE=1，则以AB所在直线为旋转轴将整个图形旋转一周所得几何体的表面积为（ ）
一个几何体的正视图、侧视图、俯视图如图所示，则该几何体的表面积为4+2π+2$\sqrt{2}$π．体积分别为$\frac{4}{3}$π．
12．在△ABC中，a=3$\sqrt{3}$，b=2，cosC=$-\frac{{\sqrt{3}}}{2}$，则c等于（ ）
| A． | 13 | B． | $\sqrt{13}$ | C． | 7 | D． | 9 |