题目内容
5.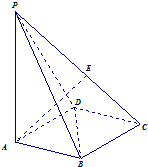 如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.
如图,底面为菱形的四棱锥P-ABCD中,PA⊥面ABCD,∠ABD=60°,E为PC上一动点,PA=AC.(1)求证BD⊥AE;
(2)当AE⊥平面PBD时,求$\frac{PE}{CE}$的值;
(3)在(2)的条件下,求AD与平面PBD所成角的正弦值.
分析 (1)结合菱形的性质,根据线面垂直推出线线垂直即可;(2)建立坐标系,设$\frac{PE}{PC}=λ>0$,根据AE⊥平面PBD,由$\overrightarrow{AE}•\overrightarrow{PD}=0$,求出λ的值即可;(3)根据AE是平面PBD的一个法向量,代入公式求出即可.
解答 解(1)菱形ABCD⇒AC⊥BD,PA⊥面ABCD⇒PA⊥BD,
又PA∩AC=A,所以BD⊥面PAC,又AE?面PAC,所以BD⊥AE;
(2)连接AC交BD于点O,以O为圆心,OA,OB分别为x,y轴,建立如图所示空间坐标系,
如图示: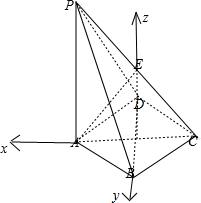 ,
,
设AB=2,则$A(\sqrt{3},0,0),C(-\sqrt{3},0,0)$,B(0,1,0),D(0,-1,0),$P(\sqrt{3},0,2\sqrt{3})$,
设$\frac{PE}{PC}=λ>0$,$E(\sqrt{3}-2\sqrt{3}λ,0,2\sqrt{3}-2\sqrt{3}λ)$,
AE⊥平面PBD,$\overrightarrow{AE}•\overrightarrow{PD}=0$,则$λ=\frac{2}{3}$,$\frac{PE}{CE}=2$;
(3)因为AE⊥平面PBD,
所以AE是平面PBD的一个法向量,取$A\overrightarrow E=(-2,0,1)$
设AD与平面PBD所成角为θ,
则$sinθ=\frac{{|\overrightarrow{AD}•\overrightarrow{AE}|}}{{|\overrightarrow{AD|}•\overrightarrow{|AE|}}}=\frac{{\sqrt{15}}}{5}$.
点评 本题考查了线面垂直的性质即判定,考查线面角问题,是一道中档题.

 小学课时特训系列答案
小学课时特训系列答案| 月份x | 1 | 2 | 3 | 4 |
| 用电量y | 45 | 40 | 30 | 25 |
| A. | 105 | B. | 51.5 | C. | 52 | D. | 52.5 |
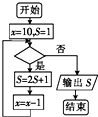
| A. | x>7? | B. | x>6? | C. | x≥6? | D. | x≤6? |
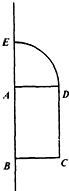 如图所示,矩形ABCD和一个圆心角为90°的扇形拼在一起,其中AB=2,BC=AE=1,则以AB所在直线为旋转轴将整个图形旋转一周所得几何体的表面积为( )
如图所示,矩形ABCD和一个圆心角为90°的扇形拼在一起,其中AB=2,BC=AE=1,则以AB所在直线为旋转轴将整个图形旋转一周所得几何体的表面积为( )