题目内容
已知数列{an}满足Sn+an=2n+1,
(1)写出a1,a2,a3,并推测an的表达式,(2)用数学归纳法证明所得的结论.
(1)写出a1,a2,a3,并推测an的表达式,(2)用数学归纳法证明所得的结论.
(1)由Sn+an=2n+1得a1= , a2=
, a2=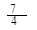 , a3=
, a3= , ∴an=
, ∴an=
(2)证明:当n=1时成立. 假设n=k时命题成立,即ak= ,
,
当n=k+1时,a1+a2+…ak+ak+1+ak+1=2(k+1)+1,
∵a1+a2+…ak =2k+1-ak, ∴2ak+1=4- , ∴ak+1=2-
, ∴ak+1=2- 成立.
成立.
根据上述知对于任何自然数n,结论成立.
 , a2=
, a2=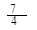 , a3=
, a3= , ∴an=
, ∴an=
(2)证明:当n=1时成立. 假设n=k时命题成立,即ak=
 ,
, 当n=k+1时,a1+a2+…ak+ak+1+ak+1=2(k+1)+1,
∵a1+a2+…ak =2k+1-ak, ∴2ak+1=4-
 , ∴ak+1=2-
, ∴ak+1=2- 成立.
成立.根据上述知对于任何自然数n,结论成立.
略

练习册系列答案
相关题目
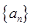 中,
中,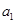 ,
,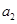 ,
,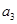 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且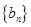 满足:
满足: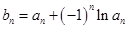 ,求数列
,求数列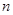 项和
项和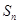 .
.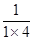 ,
,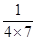 ,
,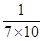 ,……,
,……,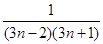 ,……
,……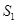 ,
,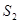 ,
,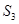 ,
,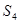
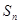 的表达式并用数学归纳法证明你的猜想。
的表达式并用数学归纳法证明你的猜想。 的公差
的公差 ,它的前
,它的前 项和为
项和为 ,若
,若 ,且
,且 ,
, ,
,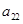 成等比数列.
成等比数列. 的前
的前 ,求证:
,求证: .
.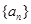 ,若点
,若点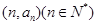 在经过点(5,3)的定直线
在经过点(5,3)的定直线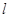 上,则数列
上,则数列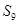 =( )
=( ) 的前四项和为14,且
的前四项和为14,且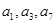 恰为等比数列
恰为等比数列 的前三项。
的前三项。 的前n项和
的前n项和
 为数列
为数列 的前n项和,若不等式
的前n项和,若不等式 对一切
对一切 恒成立,求实数
恒成立,求实数 的最小值。
的最小值。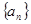 的通项公式
的通项公式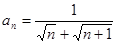 ,则该数列的前( )项之和等于
,则该数列的前( )项之和等于




 中,已知
中,已知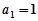 ,对任意的
,对任意的 ,有
,有 成等比数列,且公比为
成等比数列,且公比为 ,则
,则 的值为
的值为



 满足
满足 ,则数列
,则数列 的前10项和为
的前10项和为


