题目内容
((本小题满分14分)
已知等差数列 的公差
的公差 ,它的前
,它的前 项和为
项和为 ,若
,若 ,且
,且 ,
, ,
, 成等比数列.
成等比数列.
(1)求数列 的通项公式;
的通项公式;
(2)设数列 的前
的前 项和为
项和为 ,求证:
,求证: .
.
已知等差数列
 的公差
的公差 ,它的前
,它的前 项和为
项和为 ,若
,若 ,且
,且 ,
, ,
, 成等比数列.
成等比数列.(1)求数列
 的通项公式;
的通项公式; (2)设数列
 的前
的前 项和为
项和为 ,求证:
,求证: .
.(1)因为数列
 是等差数列,
是等差数列,所以
 ,
, .
.依题意,有
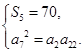 即
即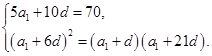
解得
 ,
, .
.所以数列
 的通项公式为
的通项公式为 (
( ).
).(2)证明:由(1)可得
 .
.所以
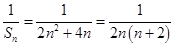
 .
.所以
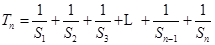

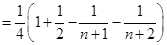
 .
.因为
 ,所以
,所以 .
.因为
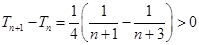 ,所以数列
,所以数列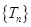 是递增数列.
是递增数列.所以
 .
.所以
 .
. 略

练习册系列答案
相关题目
 的前5项的和是 。
的前5项的和是 。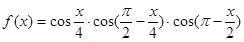 ,将函数
,将函数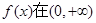 的所有极值点从小到大排成一数列,记为
的所有极值点从小到大排成一数列,记为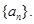
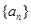 的通项公式;
的通项公式;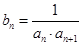 ,求数列
,求数列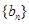 前n项和
前n项和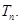
 满足:
满足: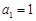 ,
,
 ,
, ; (Ⅱ)令
; (Ⅱ)令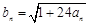 ,求数列
,求数列 的通项公式;
的通项公式; ,求证:
,求证: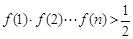 .
.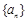 中,
中,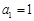 ,
,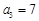 ,且
,且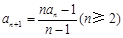 .
. 及
及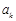 是
是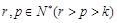 ,使
,使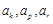 成等比数列?如存在,试分别写出
成等比数列?如存在,试分别写出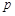 和
和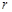 关于
关于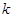 的一个表达式,并给出证明;
的一个表达式,并给出证明; ,
,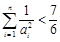 .
. 1)小问6分,(2)小分6分.)
1)小问6分,(2)小分6分.)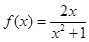 ,数列
,数列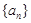 满足
满足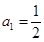 ,
,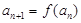 ,
,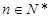 .
.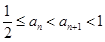 ;
;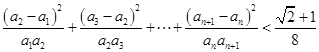 .
. 的前n项和
的前n项和 ,则
,则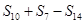 为( )
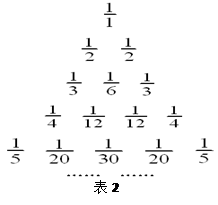
为( ) 下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)
下面的单位分数三角形(单位分数是分子为1,分母为正整数的分数),称为莱布尼兹三角形(如表2)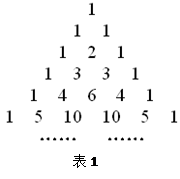
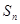 为表1中第n行各个数字之和,求
为表1中第n行各个数字之和,求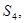
 ,并归纳出
,并归纳出