题目内容
数列 中,已知
中,已知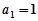 ,对任意的
,对任意的 ,有
,有 成等比数列,且公比为
成等比数列,且公比为 ,则
,则 的值为
的值为
 中,已知
中,已知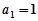 ,对任意的
,对任意的 ,有
,有 成等比数列,且公比为
成等比数列,且公比为 ,则
,则 的值为
的值为A. | B. | C. | D. |
B
依题意可得对任意的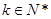 ,有
,有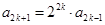 ,所以
,所以

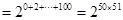
故选B
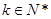 ,有
,有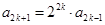 ,所以
,所以
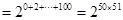
故选B

练习册系列答案
 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案
相关题目
题目内容
 中,已知
中,已知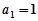 ,对任意的
,对任意的 ,有
,有 成等比数列,且公比为
成等比数列,且公比为 ,则
,则 的值为
的值为A. | B. | C. | D. |
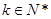 ,有
,有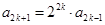 ,所以
,所以
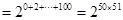

 名题金卷系列答案
名题金卷系列答案 优加精卷系列答案
优加精卷系列答案