题目内容
(本小题满分12分)
已知函数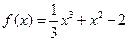 。
。
(Ⅰ)设{an}是正数组成的数列,前n项和为Sn,其中a1=3,若点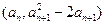 (n∈N*)在函数y=f′(x)的图象上,求证:点(n, Sn)也在y=f′(x)的图象上;
(n∈N*)在函数y=f′(x)的图象上,求证:点(n, Sn)也在y=f′(x)的图象上;
(Ⅱ)求函数f(x)在区间(a-1,a)内的极值。
已知函数
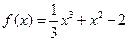 。
。(Ⅰ)设{an}是正数组成的数列,前n项和为Sn,其中a1=3,若点
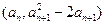 (n∈N*)在函数y=f′(x)的图象上,求证:点(n, Sn)也在y=f′(x)的图象上;
(n∈N*)在函数y=f′(x)的图象上,求证:点(n, Sn)也在y=f′(x)的图象上;(Ⅱ)求函数f(x)在区间(a-1,a)内的极值。
(Ⅰ)证明见解析。
(Ⅱ)当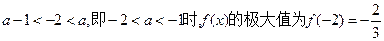 ,此时
,此时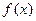 无极小值;
无极小值;
当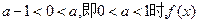 的极小值为
的极小值为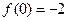 ,此时
,此时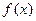 无极大值;
无极大值;
当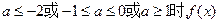 既无极大值又无极小值。
既无极大值又无极小值。
(Ⅱ)当
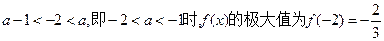 ,此时
,此时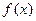 无极小值;
无极小值;当
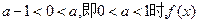 的极小值为
的极小值为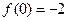 ,此时
,此时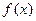 无极大值;
无极大值;当
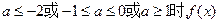 既无极大值又无极小值。
既无极大值又无极小值。(Ⅰ)证明:因为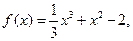 所以
所以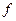 ′(x)=x2+2x,
′(x)=x2+2x,
由点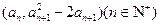 在函数y=f′(x)的图象上,
在函数y=f′(x)的图象上,
又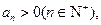 所以
所以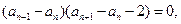
所以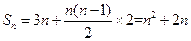 ,又因为
,又因为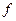 ′(n)=n2+2n,所以
′(n)=n2+2n,所以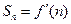 ,
,
故点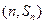 也在函数y=f′(x)的图象上.
也在函数y=f′(x)的图象上.
(Ⅱ)解: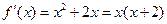 ,
,
由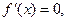 得
得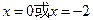 .
.
当x变化时,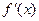 ﹑
﹑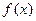 的变化情况如下表:
的变化情况如下表:
注意到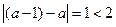 ,从而
,从而
①当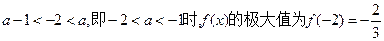 ,此时
,此时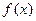 无极小值;
无极小值;
②当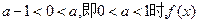 的极小值为
的极小值为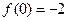 ,此时
,此时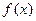 无极大值;
无极大值;
③当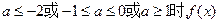 既无极大值又无极小值。
既无极大值又无极小值。
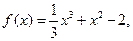 所以
所以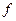 ′(x)=x2+2x,
′(x)=x2+2x,由点
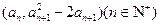 在函数y=f′(x)的图象上,
在函数y=f′(x)的图象上,又
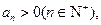 所以
所以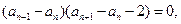
所以
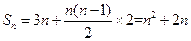 ,又因为
,又因为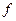 ′(n)=n2+2n,所以
′(n)=n2+2n,所以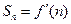 ,
,故点
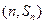 也在函数y=f′(x)的图象上.
也在函数y=f′(x)的图象上.(Ⅱ)解:
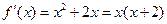 ,
,由
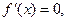 得
得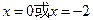 .
.当x变化时,
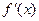 ﹑
﹑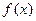 的变化情况如下表:
的变化情况如下表:| x | (-∞,-2) | -2 | (-2,0) | 0 | (0,+∞) |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | ↗ | 极大值 | ↘ | 极小值 | ↗ |
注意到
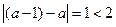 ,从而
,从而①当
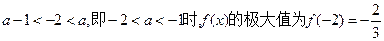 ,此时
,此时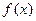 无极小值;
无极小值;②当
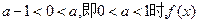 的极小值为
的极小值为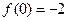 ,此时
,此时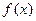 无极大值;
无极大值;③当
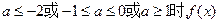 既无极大值又无极小值。
既无极大值又无极小值。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
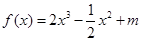 (
(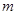 为常数)图象上
为常数)图象上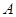 处的切线与直线
处的切线与直线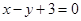 的夹角为45°,则点
的夹角为45°,则点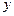 与每日产量
与每日产量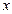 的函数关系式为
的函数关系式为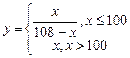 ,该工厂售出一件正品可获利
,该工厂售出一件正品可获利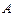 元,但生产一件次品就损失
元,但生产一件次品就损失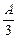 元,为了获得最大利润,日产量应定为多少?
元,为了获得最大利润,日产量应定为多少?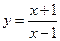 在点
在点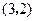 处的切线与直线
处的切线与直线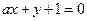 垂直,则
垂直,则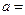 ( )
( )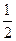
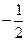
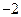
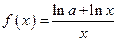 在
在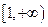 上为减函数,则实数
上为减函数,则实数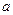 的取值范围是( )
的取值范围是( )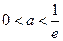
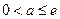
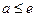
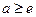
 。
。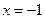 处的切线方程;
处的切线方程; ;若
;若 ..
..