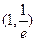题目内容
曲线y=x3-3x2+1在点(1,-1)处的切线方程为( )
| A.y=3x-4 | B.y=-3x+2 | C.y=-4x+3 | D.y=4x-5 |
B
分析:求出函数y=x3-3x2+1在x=1处的导数值,这个导数值即函数图象在该点处的切线的斜率,然后根据直线的点斜式方程求解即可.
解:由曲线y=x3-3x2+1,
所以y′=3x2-6x,
曲线y=x3-3x2+1在点(1,-1)处的切线的斜率为:y′|x=1=3(1)2-6=-3.
此处的切线方程为:y+1=-3(x-1),即y=-3x+2.
故答案为:B.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
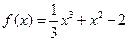 。
。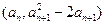 (n∈N*)在函数y=f′(x)的图象上,求证:点(n, Sn)也在y=f′(x)的图象上;
(n∈N*)在函数y=f′(x)的图象上,求证:点(n, Sn)也在y=f′(x)的图象上;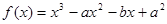 在
在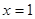 处有极值10, 则点
处有极值10, 则点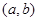 为( )
为( )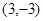
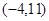
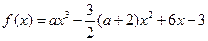 。
。 时,求函数
时,求函数 的极小值;
的极小值; 零点的个数。
零点的个数。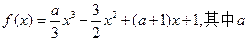 为实数。
为实数。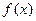 在
在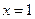 处取得极值,求
处取得极值,求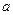 的值;
的值; 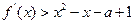 对任意
对任意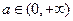 都成立,求实数
都成立,求实数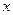 的取值范围。
的取值范围。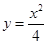 在点P(2, 1)处的切线方程为__________________________.
在点P(2, 1)处的切线方程为__________________________.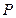 与周次
与周次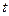 之间的函数关系;
之间的函数关系;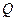 与周次
与周次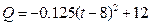 ,
,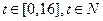 ,问该服装第几周每件销售利润最大?
,问该服装第几周每件销售利润最大?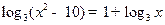 的解是 。
的解是 。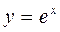 在点P处的切线斜率为e,则点P的坐标为( )
在点P处的切线斜率为e,则点P的坐标为( )