题目内容
【题目】如图,已知OPQ是半径为 ![]() 圆心角为
圆心角为 ![]() 的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α.
的扇形,C是该扇形弧上的动点,ABCD是扇形的内接矩形,记∠BOC为α. 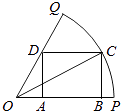
(Ⅰ)若Rt△CBO的周长为 ![]() ,求
,求 ![]() 的值.
的值.
(Ⅱ)求 ![]() 的最大值,并求此时α的值.
的最大值,并求此时α的值.
【答案】解:(Ⅰ)BC=OCsinα= ![]() sinα,OB=OCcosα=
sinα,OB=OCcosα= ![]() cosα,
cosα,
则若Rt△CBO的周长为  ,
,
则 ![]() +
+ ![]() sinα+
sinα+ ![]() cosα=
cosα=  ,
,
sinα+cosα= ![]() ,
,
平方得2sinαcosα= ![]() ,
,
即 ![]() =
= ![]() =
= ![]() ,
,
解得tanα=3(舍)或tanα= ![]() .
.
则 ![]() =
= ![]() =
= ![]() =
= 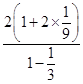 =
= ![]() .
.
(Ⅱ)在Rt△OBC中,BC=OCsinα= ![]() sinα,OB=OCcosα=
sinα,OB=OCcosα= ![]() cosα,
cosα,
在Rt△ODA中,
OA=DAtan ![]() =
= ![]() BC=
BC= ![]() sinα,
sinα,
∴AB=OB﹣OA= ![]() (cosα﹣
(cosα﹣ ![]() cosα),
cosα),
则 ![]() =|
=| ![]() |
| ![]() |=
|= ![]() (cosα﹣
(cosα﹣ ![]() cosα)
cosα) ![]() sinα
sinα ![]()
= 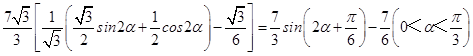
∵ ![]() ,
,
∴ ![]() ,
,
∴当 ![]() ,
,
即 ![]() 时,
时, ![]() 有最大值
有最大值 ![]() .
.
【解析】(Ⅰ)由条件利用直角三角形中的边角关系求出三角形的周长,利用三角函数的倍角公式进行化简进行求解.(Ⅱ)结合向量的数量积公式,结合三角函数的带动下进行求解.
【考点精析】本题主要考查了扇形面积公式的相关知识点,需要掌握若扇形的圆心角为![]() ,半径为
,半径为![]() ,弧长为
,弧长为![]() ,周长为
,周长为![]() ,面积为
,面积为![]() ,则
,则![]() ,
,![]() ,
,![]() 才能正确解答此题.
才能正确解答此题.

练习册系列答案
相关题目