题目内容
【题目】已知中心在坐标原点的椭圆C经过点A(2,3),且点F (2,0)为其右焦点.
(1)求椭圆C的方程和离心率e;
(2)若平行于OA的直线l与椭圆有公共点,求直线l在y轴上的截距的取值范围.
【答案】
(1)
解:由椭圆的焦点在x轴上,c=2,设椭圆方程为 ![]() ,
,
代入点A(2,3), ![]()
解得:a2=16,则b2=12,离心率e= ![]() =
= ![]()
∴椭圆方程为 ![]() ,离心率
,离心率 ![]()
(2)
解:设直线l的方程y= ![]() x+b,
x+b,
则 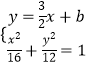 ,整理得:3x2+3bx+b2﹣12=0,
,整理得:3x2+3bx+b2﹣12=0,
由△=(3b)2﹣12(b2﹣12)≥0,解得:﹣4 ![]() ≤b≤4
≤b≤4 ![]() ,
,
直线l在y轴上的截距的取值范围[﹣4 ![]() ,4
,4 ![]() ]
]
【解析】(1)由题意c=2,设椭圆方程,将A代入椭圆方程,即可求得a的值,即可求得椭圆方程及离心率;(2)设直线方程,代入椭圆方程,由韦达定理△≥0,即可求得b的取值范围.
【考点精析】关于本题考查的椭圆的标准方程,需要了解椭圆标准方程焦点在x轴:![]() ,焦点在y轴:
,焦点在y轴:![]() 才能得出正确答案.
才能得出正确答案.

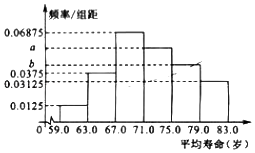
【题目】下面给出了2010年亚洲一些国家的国民平均寿命(单位:岁)
国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 | 国家 平均寿命 |
阿曼 76.1 | 泰国 73.7 | 阿富汗 59.0 | 尼泊尔 68.0 | 孟加拉国 70.1 |
(1)请补齐频率分布表,并求出相应频率分布直方图中的a,b;
分组 | 频数 | 频率 |
[59.0,63.0) | 2 | 0.05 |
[63.0,67.0) | ||
[67.0,71.0) | ||
[71.0,75.0) | 9 | 0.225 |
[75.0,7.0) | 7 | 0.175 |
[79.0,83.0] | 5 | 0.125 |
合计 | 40 | 1.00 |
(2)请根据统计思想,利用(1)中的频率分布直方图估计亚洲人民的平均寿命.