题目内容
【题目】已知椭圆两焦点 ![]() ,并且经过点
,并且经过点 ![]() .
.
(1)求椭圆的方程;
(2)若过点A(0,2)的直线l与椭圆交于不同的两点M、N(M在A、N之间),试求△OAM与△OAN面积之比的取值范围.
【答案】
(1)解:因为椭圆的焦点在x上,
所以设椭圆方程为 ![]() (a>b>0),
(a>b>0),
由定义得 ![]() +,
+,
∴a=2,b2=4﹣3=1,所以椭圆方程为 ![]()
(2)解:由题意知直线l的斜率存在且不为零,设l方程为y=kx+2(k≠0),
设M(x1,y1),N(x2,y2),
由 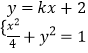 整理得(1+4k2)x2+16kx+12=0,
整理得(1+4k2)x2+16kx+12=0,
由△=256k2﹣48(1+4k2)>0,得 ![]() ;
;
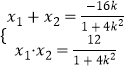 ,
,
令 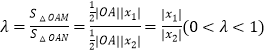 ,
,
∵x1x2>0,∴x1,x2同号,∴ ![]() ∴x1=λx2,
∴x1=λx2,
∴ 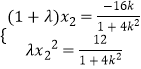 ,
,
∴ 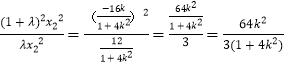
∴ ![]()
∵ ![]() ∴
∴ ![]() ,解得
,解得 ![]() ,
,
∵0<λ<1∴ ![]() ,
,
所以△OAM与△OAN面积之比的取值范围是 ![]()
【解析】(1)设椭圆方程为 ![]() (a>b>0),运用椭圆的定义,可得a=2,结合a,b,c的关系,求得b,进而得到椭圆方程;(2)设l方程为y=kx+2(k≠0),M(x1 , y1),N(x2 , y2),代入椭圆方程,运用判别式大于0和韦达定理,令
(a>b>0),运用椭圆的定义,可得a=2,结合a,b,c的关系,求得b,进而得到椭圆方程;(2)设l方程为y=kx+2(k≠0),M(x1 , y1),N(x2 , y2),代入椭圆方程,运用判别式大于0和韦达定理,令 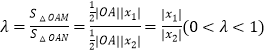 ,代入化简整理,运用不等式的性质,即可得到所求范围.
,代入化简整理,运用不等式的性质,即可得到所求范围.

 期末宝典单元检测分类复习卷系列答案
期末宝典单元检测分类复习卷系列答案【题目】某种产品的广告费支出x与销售额y(单位:百万元)之间有如下对应数据:
x | 2 | 4 | 5 | 6 | 8 |
y | 30 | 40 | 60 | 50 | 70 |
参考公式:b= 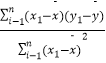 =
= 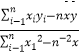 .
.
(1)画出散点图;
(2)求回归直线方程;
(3)试预测广告费支出为10百万元时,销售额多大?
【题目】假设某种设备使用的年限x(年)与所支出的维修费用y(元)有以下统计资料:
使用年限x | 2 | 3 | 4 | 5 | 6 |
维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
参考数据: ![]() ,
, ![]() ,
,
如果由资料知y对x呈线性相关关系.试求:
(1)![]() ;
;
(2)线性回归方程 ![]() =bx+a.
=bx+a.
(3)估计使用10年时,维修费用是多少?