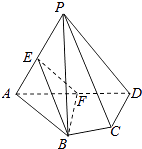
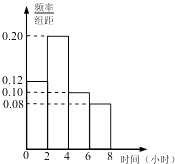
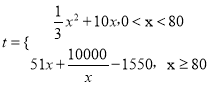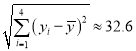题目内容
【题目】对于函数y=f（x），若在其定义域内存在x0 ， 使得x0f（x0）=1成立，则称x0为函数f（x）的“反比点”．下列函数中具有“反比点”的是
①f（x）=﹣2x+2
； ②f（x）=sinx，x∈[0，2π]；
③f（x）=x+
， x∈（0，+∞）；④f（x）=ex； ⑤f（x）=﹣2lnx．
【答案】①②④
【解析】①由
则①具有“反比点”．
②设h（x）=xsinx﹣1，∵h（0）=﹣1＜0，
，
∴h（x）=xsinx﹣1=0xsinx=1在
上有解，所以②具有“反比点”．
③由
（0，+∞），所以③不具有“反比点”；
④若xex=1令g（x）=xex﹣1，g（0）=﹣1＜0，g（1）=e﹣1＞0④具有“反比点”
⑤若
在（0，+∞）上 有解，
令h（x）=xlnxh'（x）=lnx+1=0x=e﹣1 ，
可得h（x）在x=e﹣1有最小值﹣e﹣1 ， 而
， 所以⑤不具有“反比点”，
所以答案是：①②④
【考点精析】解答此题的关键在于理解函数的值的相关知识，掌握函数值的求法：①配方法(二次或四次)；②“判别式法”；③反函数法；④换元法；⑤不等式法；⑥函数的单调性法．
练习册系列答案
相关题目
