��Ŀ����
����Ŀ��ij��˾Ϊ��ȷ�ذ����г������ò�Ʒ�����ƻ����Թ�ȥ��������ݽ��������õ��˵�![]() ����������
����������![]() (��λ�����)֮��Ĺ�ϵ�����
(��λ�����)֮��Ĺ�ϵ�����


(��)��ͼ�л����������ݵ�ɢ��ͼ��
(��)����(��)�е�ɢ��ͼ���![]() ��
��![]() �Ļع�ģ�ͣ��������ϵ������˵����
�Ļع�ģ�ͣ��������ϵ������˵����
(��)����![]() ����
����![]() �Ļع鷽�̣�Ԥ���5���������ԼΪ���٣�.
�Ļع鷽�̣�Ԥ���5���������ԼΪ���٣�.
��ע���ο����ݣ� 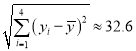 ��
�� ![]() ��
�� ![]() .
.
�ο���ʽ�����ϵ�� ��
��
�ع鷽��![]() ��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��
��б�ʺͽؾ����С���˷����ƹ�ʽ�ֱ�Ϊ��
 ��
�� ![]() .
.
���𰸡�(��)ɢ��ͼ��������(��)�𰸼�������(��) 71���.
�����������������
(��) ��������������ɢ��ͼ;
(��) �������ṩ�������빫ʽ���![]() ��
��![]() �����ϵ��r,���ɵó�����;
�����ϵ��r,���ɵó�����;
(��) ���������ṩ������,�ֱ����![]() ��ֵ,��ɵûع�ֱ�߷���,�ٽ�
��ֵ,��ɵûع�ֱ�߷���,�ٽ�![]() ����ع�ֱ�߷��̿ɵý���.
����ع�ֱ�߷��̿ɵý���.
���������
(��)����ɢ��ͼ��ͼ��

(��)��(��)ɢ��ͼ��֪��������·ֲ���һ��ֱ�߸������������������ο����ݵã�
![]() ��
�� ![]() ��
�� ![]() ��
��  ��
�� ![]() ��
�� ![]() ��
��  ��
��
 .
.
��![]() ��
��![]() �����ϵ������Ϊ0.9996��˵��
�����ϵ������Ϊ0.9996��˵��![]() ��
��![]() ��������س̶��൱��
��������س̶��൱��
����������Իع�ģ�����![]() ��
��![]() �Ĺ�ϵ.
�Ĺ�ϵ.
(��)��(��)֪�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
 ��
�� ![]() ��
��
��![]() ����
����![]() �Ļع�ֱ�߷���Ϊ
�Ļع�ֱ�߷���Ϊ![]() ��
��
��![]() ʱ��
ʱ�� ![]() ��
��
���Ե�5���������ԼΪ71���.

 ��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�
��ͼͼ�麮����ҵ������ҵ���ִ�ѧ������ϵ�д�����Ŀ��ij�����̴����ˮ����ֳ������һ��С��Ϻ���������ȡ40ֻ����ͳ�ƣ�����������ͳ�ƽ������ͼ��

��1�����¼�![]() Ϊ����������С��Ϻ����ȡһֻ������������35
Ϊ����������С��Ϻ����ȡһֻ������������35![]() ��С��Ϻ������
��С��Ϻ������![]() �Ĺ���ֵ��
�Ĺ���ֵ��
��2������������С��Ϻ100ǧ�ˣ��Թ�������С��Ϻ��������
��3��Ϊ��Ӧ�г������˽�����С��Ϻ�ĿڸУ��þ����̽���40ֻС��Ϻ�ֳ������ȼ������±���
�ȼ� | һ��Ʒ | ����Ʒ | ����Ʒ |
������ |
|
|
|
���ֲ������ȡ10ֻ���������ȡ3ֻƷ������![]() Ϊ�鵽����Ʒ����������鵽����Ʒ��������
Ϊ�鵽����Ʒ����������鵽����Ʒ��������

