Question

【题目】如图，在四棱锥ABCD﹣PGFE中，底面ABCD是直角梯形，侧棱垂直于底面，AB∥DC，∠ABC=45°，DC=1，AB=2，PA=1．
（Ⅰ）求PD与BC所成角的大小；
（Ⅱ）求证：BC⊥平面PAC；
（Ⅲ）求二面角A﹣PC﹣D的大小．

Answer 1

【答案】解：（Ⅰ）取的AB中点H，连接DH，易证BH∥CD，且BH=CD
所以四边形BHDC为平行四边形，所以BC∥DH
所以∠PDH为PD与BC所成角
因为四边形，ABCD为直角梯形，且∠ABC=45°，所以⊥DA⊥AB
又因为AB=2DC=2，所以AD=1，因为Rt△PAD、Rt△DAH、Rt△PAH都为等腰直角三角形，
所以PD=DH=PH=，故∠PDH=60°
（Ⅰ）连接CH，则四边形ADCH为矩形，∴AH=DC 又AB=2，∴BH=1
在Rt△BHC中，∠ABC=45°，∴CH=BH=1，CB=∴AD=CH=1，AC=
∴AC2+BC2=AB2∴BC⊥AC 又PA平面ABCD∴PA⊥BC
∵PA∩AC=A∴BC⊥平面PAC.
（Ⅲ）如图，分别以AD、AB、AP为x轴，y轴，z轴
建立空间直角坐标系，则由题设可知：
A（0，0，0），P（0，0，1），C（1，1，0），D（1，0，0），
∴=（0，0，1），=（1，1，﹣1
设m=（a，b，c）为平面PAC的一个法向量，则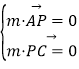，即
设a=1，则b=﹣1，∴m=（1，﹣1，0）
同理设n=（x，y，z） 为平面PCD的一个法向量，求得n=（1，1，1）
∴cos<m,n>=
所以二面角A﹣PC﹣D为60°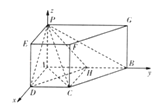

【解析】（1）取的AB中点H，易证∠PDH为PD与BC所成角，解三角形可得；
（2）由已知结合线面垂直的判定可得：
（3）坐标法求得平面的法向量，由向量的夹角可得二面角的大小．
【考点精析】关于本题考查的异面直线及其所成的角和直线与平面垂直的判定，需要了解异面直线所成角的求法：1、平移法：在异面直线中的一条直线中选择一特殊点，作另一条的平行线；2、补形法：把空间图形补成熟悉的或完整的几何体，如正方体、平行六面体、长方体等，其目的在于容易发现两条异面直线间的关系；一条直线与一个平面内的两条相交直线都垂直，则该直线与此平面垂直；注意点：a)定理中的“两条相交直线”这一条件不可忽视；b)定理体现了“直线与平面垂直”与“直线与直线垂直”互相转化的数学思想才能得出正确答案．