题目内容
【题目】(1)试比较![]() 与
与![]() 的大小.
的大小.
(2)若函数![]() 的两个零点分别为
的两个零点分别为![]() ,
,![]() ,
,
①求![]() 的取值范围;
的取值范围;
②证明:![]() .
.
【答案】(1)答案见解析.(2)①![]() .②证明见解析
.②证明见解析
【解析】
(1)设![]() ,然后利用导数求出
,然后利用导数求出![]() 的单调性,然后结合函数值即可比较出大小;
的单调性,然后结合函数值即可比较出大小;
(2)①利用导数求出![]() 的最小值即可;
的最小值即可;
②不妨设![]() ,则
,则![]() ,结合(1)中结论可推出
,结合(1)中结论可推出![]() ,
,![]() ,然后可得
,然后可得![]() ,将其分解因式可证明
,将其分解因式可证明![]() .
.
(1)设![]() ,
,
则![]() ,
,
故![]() 在
在![]() 上单调递减.
上单调递减.
因为![]() ,
,
所以当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .
.
即当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() ;
;
当![]() 时,
时,![]() .
.
(2)①因为![]() ,所以
,所以![]() ,
,
令![]() ,得
,得![]() ;令
;令![]() ,得
,得![]() ,
,
则![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增,
上单调递增,
故![]() .
.
因为![]() 有两个零点,所以
有两个零点,所以![]() ,即
,即![]() .
.
因为![]() ,
,![]() ,
,
所以当![]() 有两个零点时,
有两个零点时,![]() 的取值范围为
的取值范围为![]() .
.
②证明:因为![]() ,
,![]() 是
是![]() 的两个零点,
的两个零点,
不妨设![]() ,则
,则![]() .
.
因为![]() ,
,![]() ,
,
所以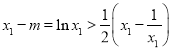 ,
,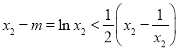 ,
,
即![]() ,
,![]() ,
,
则![]() ,即
,即![]() ,
,
即![]() .
.
因为![]() ,所以
,所以![]() ,则
,则![]() ,即
,即![]() .
.

练习册系列答案
相关题目
【题目】从集市上买回来的蔬菜仍存有残留农药,食用时需要清洗数次,统计表中的![]() 表示清洗的次数,
表示清洗的次数,![]() 表示清洗
表示清洗![]() 次后
次后![]() 千克该蔬菜残留的农药量(单位:微克).
千克该蔬菜残留的农药量(单位:微克).
x | 1 | 2 | 3 | 4 | 5 |
y | 4.5 | 2.2 | 1.4 | 1.3 | 0.6 |
(1)在如图的坐标系中,描出散点图,并根据散点图判断,![]() 与
与![]() 哪一个适宜作为清洗
哪一个适宜作为清洗![]() 次后
次后![]() 千克该蔬菜残留的农药量的回归方程类型;(给出判断即可,不必说明理由)
千克该蔬菜残留的农药量的回归方程类型;(给出判断即可,不必说明理由)

(2)根据判断及下面表格中的数据,建立![]() 关于
关于![]() 的回归方程;
的回归方程;
表中![]() ,
,![]() .
.
|
|
|
|
|
| |
3 | 2 | 0.12 | 10 | 0.09 | -8.7 | 0.9 |
(3)对所求的回归方程进行残差分析.
附:①线性回归方程![]() 中系数计算公式分别为
中系数计算公式分别为 ,
,![]() ;
;
② ,
,![]() 说明模拟效果非常好;
说明模拟效果非常好;
③![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.