题目内容
【题目】设a>0,0≤x<2π,若函数y=cos2x-asinx+b的最大值为0,最小值为-4,试求a与b的值,并求使y取得最大值和最小值时的x值.
【答案】![]() ,当
,当![]() 时,y取得最小值;当
时,y取得最小值;当![]() 时,y取得最大值
时,y取得最大值
【解析】试题分析:
利用题意得到关于实数a,b的方程组,求解方程组可得![]() ,结合函数的解析式和三角函数的性质可得当
,结合函数的解析式和三角函数的性质可得当![]() 时,y取得最小值;当
时,y取得最小值;当![]() 时,y取得最大值.
时,y取得最大值.
试题解析:
f(x)=y=cos2x-asinx+b=-sin2x-asinx+b+1=-![]() +
+![]()
令t=sinx,则![]() ,因为a>0所以-
,因为a>0所以-![]() <0,
<0,
(ⅰ)当![]() ,即0<a≤2时ymax=
,即0<a≤2时ymax= ![]() =
=![]() =0①
=0①
ymin=f(1)=b-a=-4②
由①②解得![]() 或
或![]() (舍去)
(舍去)
(ⅱ)当-![]() ,即a>2时ymax=f(-1)=a+b=0③ymin=f(1)=b-a=-4④
,即a>2时ymax=f(-1)=a+b=0③ymin=f(1)=b-a=-4④
由③④解得![]() (舍去)
(舍去)
综上, ![]() ,
,
∴f(x)=cos2x-2sinx-2=-(sinx+1)2
当![]() 时,y取得最小值;当
时,y取得最小值;当![]() 时,y取得最大值.
时,y取得最大值.

 阅读快车系列答案
阅读快车系列答案【题目】某大型科学竞技真人秀节目挑选选手的方式为:不但要对选手的空间感知、照相式记忆能力进行考核,而且要让选手经过名校最权威的脑力测试,120分以上才有机会入围.某重点高校准备调查脑力测试成绩是否与性别有关,在该高校随机抽取男、女学生各100名,然后对这200名学生进行脑力测试.规定:分数不小于120分为“入围学生”,分数小于120分为“未入围学生”.已知男生入围24人,女生未入围80人.
(1)根据题意,填写下面的2×2列联表,并根据列联表判断是否有95%以上的把握认为脑力测试后是否为“入围学生”与性别有关;
性别 | 入围人数 | 未入围人数 | 总计 |
男生 | |||
女生 | |||
总计 |
(2)用分层抽样的方法从“入围学生”中随机抽取11名学生,求这11名学生中男、女生人数;若抽取的女生的脑力测试分数各不相同(每个人的分数都是整数),分别求这11名学生中女生测试分数平均分的最小值.
|
|
|
|
|
|
|
|
|
|
附: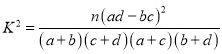 ,其中
,其中![]() .
.
【题目】为调查某公司五类机器的销售情况,该公司随机收集了一个月销售的有关数据,公司规定同一类机器销售价格相同,经分类整理得到下表:
机器类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 |
销售总额(万元) |
|
|
|
|
|
销售量(台) |
|
|
|
|
|
利润率 |
|
|
|
|
|
利润率是指:一台机器销售价格减去出厂价格得到的利润与该机器销售价格的比值.
(Ⅰ)从该公司本月卖出的机器中随机选一台,求这台机器利润率高于0.2的概率;
(Ⅱ)从该公司本月卖出的销售单价为20万元的机器中随机选取![]() 台,求这两台机器的利润率不同的概率;
台,求这两台机器的利润率不同的概率;
(Ⅲ)假设每类机器利润率不变,销售一台第一类机器获利![]() 万元,销售一台第二类机器获利
万元,销售一台第二类机器获利![]() 万元,…,销售一台第五类机器获利
万元,…,销售一台第五类机器获利![]() ,依据上表统计数据,随机销售一台机器获利的期望为
,依据上表统计数据,随机销售一台机器获利的期望为![]() ,设
,设![]() ,试判断
,试判断![]() 与
与![]() 的大小.(结论不要求证明)
的大小.(结论不要求证明)