题目内容
【题目】已知函数![]() .
.
(1)讨论![]() 的单调性;
的单调性;
(2)当![]() 时,
时,![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)求出函数![]() 的导数,分
的导数,分![]() 和
和![]() 两种情况讨论,分析导数
两种情况讨论,分析导数![]() 的符号变化,即可求出函数
的符号变化,即可求出函数![]() 的单调区间;
的单调区间;
(2)问题变形为![]() ,令
,令![]() ,由题意得出
,由题意得出![]() ,根据函数
,根据函数![]() 的单调性确定
的单调性确定![]() 的范围即可.
的范围即可.
(1)![]() ,定义域为
,定义域为![]() 且
且![]() .
.
①当![]() 时,则
时,则![]() ,则函数
,则函数![]() 在
在![]() 上单调递增;
上单调递增;
②当![]() 时,由
时,由![]() ,得
,得![]() ,得
,得![]() .
.
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减;
单调递减;
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增.
单调递增.
此时,函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() .
.
综上所述,当![]() 时,函数
时,函数![]() 的单调递增区间为
的单调递增区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调减区间为
的单调减区间为![]() ,单调增区间为
,单调增区间为![]() ;
;
(2)![]() 变形为
变形为![]() ,
,
令![]() ,定义域为
,定义域为![]() ,且
,且![]() ,
,
![]() .
.
①当![]() 时,对任意的
时,对任意的![]() ,
,![]() ,函数
,函数![]() 在区间
在区间![]() 上为增函数,
上为增函数,
此时,![]() ,合乎题意;
,合乎题意;
②当![]() 时,则函数
时,则函数![]() 在
在![]() 上的单调减区间为
上的单调减区间为![]() ,单调增区间为
,单调增区间为![]() .
.
(i)当![]() 时,即当
时,即当![]() 时,则函数
时,则函数![]() 在区间
在区间![]() 上为增函数,
上为增函数,
此时![]() ,则函数
,则函数![]() 在区间
在区间![]() 上为增函数.
上为增函数.
此时,![]() ,合乎题意;
,合乎题意;
(ii)当![]() 时,即当
时,即当![]() 时,则函数
时,则函数![]() 在区间
在区间![]() 上单调递减,在区间
上单调递减,在区间![]() 上单调递增,所以,
上单调递增,所以,![]() ,
,
又![]() ,所以,函数
,所以,函数![]() 在区间
在区间![]() 上单调递减,
上单调递减,
当![]() 时,
时,![]() ,不合乎题意.
,不合乎题意.
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.

【题目】为调查某公司五类机器的销售情况,该公司随机收集了一个月销售的有关数据,公司规定同一类机器销售价格相同,经分类整理得到下表:
机器类型 | 第一类 | 第二类 | 第三类 | 第四类 | 第五类 |
销售总额(万元) |
|
|
|
|
|
销售量(台) |
|
|
|
|
|
利润率 |
|
|
|
|
|
利润率是指:一台机器销售价格减去出厂价格得到的利润与该机器销售价格的比值.
(Ⅰ)从该公司本月卖出的机器中随机选一台,求这台机器利润率高于0.2的概率;
(Ⅱ)从该公司本月卖出的销售单价为20万元的机器中随机选取![]() 台,求这两台机器的利润率不同的概率;
台,求这两台机器的利润率不同的概率;
(Ⅲ)假设每类机器利润率不变,销售一台第一类机器获利![]() 万元,销售一台第二类机器获利
万元,销售一台第二类机器获利![]() 万元,…,销售一台第五类机器获利
万元,…,销售一台第五类机器获利![]() ,依据上表统计数据,随机销售一台机器获利的期望为
,依据上表统计数据,随机销售一台机器获利的期望为![]() ,设
,设![]() ,试判断
,试判断![]() 与
与![]() 的大小.(结论不要求证明)
的大小.(结论不要求证明)
【题目】统计与人类活动息息相关,我国从古代就形成了一套关于统计和整理数据的方法.据宋元时代学者马端临所著的《文献通考》记载,宋神宗熙宁年间(公元1068-1077年),天下诸州商税岁额:四十万贯以上者三,二十万贯以上者五,十万贯以上者十九……五千贯以下者七十三,共计三百十一.由这段内容我们可以得到如下的统计表格:
分组(万贯) |
|
|
|
|
|
|
|
| 合计 |
合计 | 73 | 35 | 95 | 51 | 30 | 19 | 5 | 3 | 311 |
则宋神宗熙宁年间各州商税岁额(单位:万贯)的中位数大约为( )
A.0.5B.2C.5D.10
【题目】某省即将实行新高考,不再实行文理分科.某校为了研究数学成绩优秀是否对选择物理有影响,对该校2018级的1000名学生进行调查,收集到相关数据如下:
(1)根据以上提供的信息,完成![]() 列联表,并完善等高条形图;
列联表,并完善等高条形图;
选物理 | 不选物理 | 总计 | |
数学成绩优秀 | |||
数学成绩不优秀 | 260 | ||
总计 | 600 | 1000 |
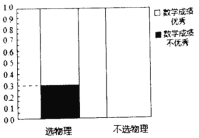
(2)能否在犯错误的概率不超过0.05的前提下认为数学成绩优秀与选物理有关?
附: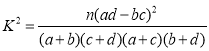
临界值表:
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |