ΧβΡΩΡΎ»ί
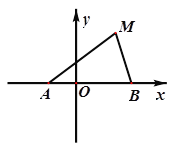
ΓΨΧβΡΩΓΩ‘≠ ΦΒΡΈΟœψ≥ωœ÷‘ΎΥΈ¥ζ.ΗυΨίΥΈ¥ζΟΑΥ’ιχ÷°Οϊ±ύ–¥ΒΡΓΕΗώΈο¥÷ΧΗΓΖΦ«‘ΊΘΚΓΑΕΥΈγ ±Θ§÷ϋΗΓΤΦΘ§“θΗ…Θ§Φ”–έΜΤΘ§Ής÷Ϋ≤χœψΘ§…’÷°Θ§ΡήλνΈΟ≥φ.Γ±»γΆΦΘ§ΈΣΡ≥–Θ ΐ―ß–Υ»Λ–ΓΉι”Ο ΐ―ß»μΦΰ÷ΤΉςΒΡΓΑ¬ί–ΐΈΟœψΓ±Θ§Μ≠Ζ®»γœ¬:‘ΎΥ°ΤΫ÷±œΏ![]() …œ»Γ≥ΛΕ»ΈΣ1ΒΡœΏΕΈ
…œ»Γ≥ΛΕ»ΈΣ1ΒΡœΏΕΈ![]() Θ§Ήω“ΜΗωΒ»±Ώ»ΐΫ«–Έ
Θ§Ήω“ΜΗωΒ»±Ώ»ΐΫ«–Έ![]() Θ§»ΜΚσ“‘Βψ
Θ§»ΜΚσ“‘Βψ![]() ΈΣ‘≤–ΡΘ§
ΈΣ‘≤–ΡΘ§![]() ΈΣΑκΨΕΡφ ±’κΜ≠‘≤ΜΓΘ§ΫΜœΏΕΈ
ΈΣΑκΨΕΡφ ±’κΜ≠‘≤ΜΓΘ§ΫΜœΏΕΈ![]() ΒΡ―”≥ΛœΏ”ΎΒψ
ΒΡ―”≥ΛœΏ”ΎΒψ![]() Θ§‘Ό“‘Βψ
Θ§‘Ό“‘Βψ![]() ΈΣ‘≤–ΡΘ§
ΈΣ‘≤–ΡΘ§![]() ΈΣΑκΨΕΡφ ±’κΜ≠‘≤ΜΓΘ§ΫΜœΏΕΈ
ΈΣΑκΨΕΡφ ±’κΜ≠‘≤ΜΓΘ§ΫΜœΏΕΈ![]() ΒΡ―”≥ΛœΏ”ΎΒψ
ΒΡ―”≥ΛœΏ”ΎΒψ![]() Θ§“‘¥ΥάύΆΤΘ§Β±ΒΟΒΫΒΡΓΑ¬ί–ΐΈΟœψΓ±”κ÷±œΏ
Θ§“‘¥ΥάύΆΤΘ§Β±ΒΟΒΫΒΡΓΑ¬ί–ΐΈΟœψΓ±”κ÷±œΏ![]() «Γ”–
«Γ”–![]() ΗωΫΜΒψ ±Θ§ΓΑ¬ί–ΐΈΟœψΓ±ΒΡΉή≥ΛΕ»ΒΡΉν–Γ÷ΒΈΣΘ® Θ©
ΗωΫΜΒψ ±Θ§ΓΑ¬ί–ΐΈΟœψΓ±ΒΡΉή≥ΛΕ»ΒΡΉν–Γ÷ΒΈΣΘ® Θ©
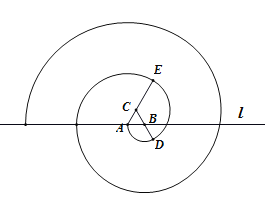
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
ΓΨ¥πΑΗΓΩA
ΓΨΫβΈωΓΩ
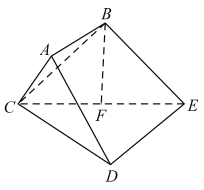
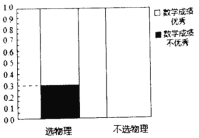
ΗυΨίΜ≠‘≤ΜΓΒΡΙφ¬…ΘΚΖ÷±π“‘BΘ§CΘ§AΈΣ‘≤–ΡΘ§≥ιœσΑκΨΕ≥ΛΕ»ΒΡ ΐΝ–Θ§Ος»Ζ‘≤ΜΓ”κ÷±œΏΒΡΫΜΒψ«ιΩωΘ§‘ΌΗυΨίΒ±ΓΑ¬ί–ΐΈΟœψΓ±”κ÷±œΏ![]() «Γ”–
«Γ”–![]() ΗωΫΜΒψ ±Θ§»τ ΙΓΑ¬ί–ΐΈΟœψΓ±ΒΡΉή≥ΛΕ»Ήν–ΓΘ§»ΖΕ® ΐΝ–ΒΡœν ΐΘ§«σΒΟΉνΚσ‘≤ΜΓΒΡΑκΨΕΦ¥Ω….
ΗωΫΜΒψ ±Θ§»τ ΙΓΑ¬ί–ΐΈΟœψΓ±ΒΡΉή≥ΛΕ»Ήν–ΓΘ§»ΖΕ® ΐΝ–ΒΡœν ΐΘ§«σΒΟΉνΚσ‘≤ΜΓΒΡΑκΨΕΦ¥Ω….
»γΆΦΥυ ΨΘΚ
Β±“‘BΈΣ‘≤–ΡΘ§ΑκΨΕΈΣΘΚ1Θ§4Θ§7Θ§10Θ§Γ≠≥ΐΤπΒψΆβΘ§”κ÷±œΏΈόΫΜΒψΘ§ΔΌ
Β±“‘CΈΣ‘≤–ΡΘ§ΑκΨΕΈΣΘΚ2Θ§5Θ§8Θ§11Θ§Γ≠”κ÷±œΏ”–“ΜΗωΒψΘ§ΔΎ
Β±“‘AΈΣ‘≤–ΡΘ§ΑκΨΕΈΣΘΚ3Θ§6Θ§9Θ§12Θ§Γ≠≥ΐ÷’ΒψΘ®Φ¥ΔΌΒΡΤπΒψΘ§ΒψA≥ΐΆβΘ©ΆβΘ§”κ÷±œΏΈόΫΜΒψΘ§Δέ
Υυ“‘Β±ΓΑ¬ί–ΐΈΟœψΓ±”κ÷±œΏ![]() «Γ”–
«Γ”–![]() ΗωΫΜΒψ ±Θ§»τ ΙΓΑ¬ί–ΐΈΟœψΓ±ΒΡΉή≥ΛΕ»Ήν–ΓΘ§
ΗωΫΜΒψ ±Θ§»τ ΙΓΑ¬ί–ΐΈΟœψΓ±ΒΡΉή≥ΛΕ»Ήν–ΓΘ§
‘ρΆξ≥…’ϊ ΐΗω―≠ΜΖΘ§
Υυ“‘“‘BΈΣ‘≤–ΡΒΡΜΓ”κ÷±œΏ÷Μ”–ΫΜΒψAΘ§“‘CΈΣ‘≤–ΡΒΡΜΓ”κ÷±œΏ10ΗωΫΜΒψΘ§“‘AΈΣ‘≤–ΡΒΡΜΓ”κ÷±œΏ”–10ΗωΫΜΒψΘ§
Φ¥ ΐΝ–ΔΎ”–10œνΘ§ ΐΝ–Δέ”–10œνΘ§
Υυ“‘ΉνΚσ“ΜΗω‘≤ΜΓΒΡΑκΨΕΈΣ![]() Θ§
Θ§
Υυ“‘ΓΑ¬ί–ΐΈΟœψΓ±ΒΡΉή≥ΛΕ»ΒΡΉν–Γ÷ΒΈΣ![]() .
.
Ι ―ΓΘΚA

 Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗ
Οϊ–ΘΩΈΧΟœΒΝ–¥πΑΗΓΨΧβΡΩΓΩΡ≥ΒΞΈΜ‘Ύ2019Ρξ÷Ί―τΫΎΉι÷·50ΟϊΆΥ–ί÷ΑΙΛΘ®Ρ–ΓΔ≈°Ης25ΟϊΘ©¬Ο”Έ,ΆΥ–ί÷ΑΙΛΩ…“‘―Γ‘ώΒΫΦΉΓΔ““ΝΫΗωΨΑΒψΤδ÷–“ΜΗω»Ξ¬Ο”Έ.ΥϊΟ«Ήν÷’―Γ‘ώΒΡΨΑΒψΒΡΫαΙϊ»γœ¬±μΘΚ
Ρ––‘ | ≈°–‘ | |
ΦΉΨΑΒψ | 20 | 10 |
““ΨΑΒψ | 5 | 15 |
Θ®1Θ©Ψί¥ΥΉ ΝœΖ÷Έω, «Ζώ”–![]() ΒΡΑ―Έ’»œΈΣ―Γ‘ώΡΡΗωΨΑΒψ”κ–‘±π”–ΙΊΘΩ
ΒΡΑ―Έ’»œΈΣ―Γ‘ώΡΡΗωΨΑΒψ”κ–‘±π”–ΙΊΘΩ
Θ®2Θ©Α¥’’”Έάά≤ΜΆ§ΨΑΒψ”ΟΖ÷≤ψ≥ι―υΒΡΖΫΖ®,‘Ύ≈°÷ΑΙΛ÷–―Γ»Γ5»Υ,‘Ό¥”’β5»Υ÷–ΥφΜζ≥ι»Γ2»ΥΫχ––≤…ΖΟ,«σ’β2»Υ”ΈάάΒΡΨΑΒψ≤ΜΆ§ΒΡΗ≈¬ .
ΗΫΘΚ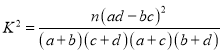 ,
,![]() .
.
PΘ® | 0.010 | 0.005 | 0.001 |
k | 6.635 | 7.879 | 10.828 |
ΓΨΧβΡΩΓΩΡ≥ ΓΦ¥ΫΪ Β–––¬ΗΏΩΦΘ§≤Μ‘Ό Β––ΈΡάμΖ÷ΩΤ.Ρ≥–ΘΈΣΝΥ―–ΨΩ ΐ―ß≥…Φ®”≈–ψ «ΖώΕ‘―Γ‘ώΈοάμ”–”ΑœλΘ§Ε‘ΗΟ–Θ2018ΦΕΒΡ1000Οϊ―ß…ζΫχ––Βς≤ιΘ§ ’Φ·ΒΫœύΙΊ ΐΨί»γœ¬ΘΚ
Θ®1Θ©ΗυΨί“‘…œΧαΙ©ΒΡ–≈œΔΘ§Άξ≥…![]() Ν–ΝΣ±μΘ§≤ΔΆξ…ΤΒ»ΗΏΧθ–ΈΆΦΘΜ
Ν–ΝΣ±μΘ§≤ΔΆξ…ΤΒ»ΗΏΧθ–ΈΆΦΘΜ
―ΓΈοάμ | ≤Μ―ΓΈοάμ | ΉήΦΤ | |
ΐ―ß≥…Φ®”≈–ψ | |||
ΐ―ß≥…Φ®≤Μ”≈–ψ | 260 | ||
ΉήΦΤ | 600 | 1000 |
Θ®2Θ©ΡήΖώ‘ΎΖΗ¥μΈσΒΡΗ≈¬ ≤Μ≥§Ιΐ0.05ΒΡ«ΑΧαœ¬»œΈΣ ΐ―ß≥…Φ®”≈–ψ”κ―ΓΈοάμ”–ΙΊΘΩ
ΗΫΘΚ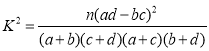
ΝΌΫγ÷Β±μΘΚ
| 0.10 | 0.05 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 6.635 | 7.879 | 10.828 |
ΓΨΧβΡΩΓΩ“Μ“ϊΝœΒξ÷ΤΉςΝΥ“ΜΩν–¬“ϊΝœΘ§ΈΣΝΥΫχ––ΚœάμΕ®Φέœ»Ϋχ–– ‘œζ έΘ§ΤδΒΞΦέ![]() Θ®‘ΣΘ©”κœζΝΩ
Θ®‘ΣΘ©”κœζΝΩ![]() Θ®±≠Θ©ΒΡœύΙΊ ΐΨί»γœ¬±μΘΚ
Θ®±≠Θ©ΒΡœύΙΊ ΐΨί»γœ¬±μΘΚ
ΒΞΦέ | 8.5 | 9 | 9.5 | 10 | 10.5 |
œζΝΩ | 120 | 110 | 90 | 70 | 60 |
Θ®1Θ©“―÷ΣœζΝΩ![]() ”κΒΞΦέ
”κΒΞΦέ![]() ΨΏ”–œΏ–‘œύΙΊΙΊœΒΘ§«σ
ΨΏ”–œΏ–‘œύΙΊΙΊœΒΘ§«σ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘΜ
ΒΡœΏ–‘ΜΊΙιΖΫ≥ΧΘΜ
Θ®2Θ©»τΗΟΩν–¬“ϊΝœΟΩ±≠ΒΡ≥…±ΨΈΣ8‘ΣΘ§ ‘œζ έΫα χΚσΘ§«κάϊ”ΟΘ®1Θ©Υυ«σΒΡœΏ–‘ΜΊΙιΖΫ≥Χ»ΖΕ®ΒΞΦέΕ®ΈΣΕύ…Ό‘Σ ±Θ§œζ έΒΡάϊ»σΉν¥σΘΩΘ®ΫαΙϊΥΡ…αΈε»κ±ΘΝτΒΫ’ϊ ΐΘ©
ΗΫΘΚœΏ–‘ΜΊΙιΖΫ≥Χ![]() ÷––±¬ ΚΆΫΊΨύΉν–ΓΕΰ¹\Ζ®ΙάΦΤΦΤΥψΙΪ ΫΘΚ
÷––±¬ ΚΆΫΊΨύΉν–ΓΕΰ¹\Ζ®ΙάΦΤΦΤΥψΙΪ ΫΘΚ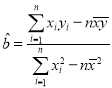 Θ§
Θ§![]() Θ§
Θ§![]() Θ§
Θ§![]() .
.