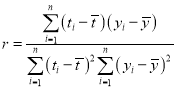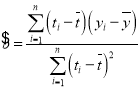题目内容
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,且B是A,C的等差中项.
(1)若![]() ,求边c的值;
,求边c的值;
(2)设t=sinAsinC,求t的取值范围.
【答案】(1)![]() .(2)
.(2)![]()
【解析】
(1)由已知利用等差中项的性质,三角形内角和定理可求B的值,进而根据余弦定理可得c2﹣3c﹣4=0,解方程可得c的值.
(2)由已知利用三角函数恒等变换的应用,可求t=![]() sin(2A﹣
sin(2A﹣![]() ,根据正弦函数的性质可求其取值范围.
,根据正弦函数的性质可求其取值范围.
(1)∵B是A,C的等差中项,
∴2B=A+C,
∵A+B+C=π,
∴B=![]() ,
,
∵b=![]() ,a=3,又b2=a2+c2﹣2accosB,
,a=3,又b2=a2+c2﹣2accosB,
∴c2﹣3c﹣4=0,
解得c=4,或c=﹣1(舍去),故c=4.
(2)∵A+C=![]() ,
,
∴t=sinAsin(![]() ﹣A)=sinA(
﹣A)=sinA(![]() cosA+
cosA+![]() sinA)=
sinA)=![]() sin(2A﹣
sin(2A﹣![]() ,
,
∵A∈(0,![]() ),2A﹣
),2A﹣![]() ∈(﹣
∈(﹣![]() ),
),
sin(2A﹣![]() )∈(
)∈(![]() ,1],
,1],
故t的取值范围为(0,![]() ].
].

【题目】某大型歌手选秀活动,过程分为初赛、复赛和决赛.经初赛进入复赛的40名选手被平均分成甲、乙两个班,由组委会聘请两位导师各负责一个班进行声乐培训.下图是根据这40名选手参加复赛时获得的100名大众评审的支持票数制成的茎叶图.赛制规定:参加复赛的40名选手中,获得的支持票数不低于85票的可进入决赛,其中票数不低于95票的选手在决赛时拥有“优先挑战权”.
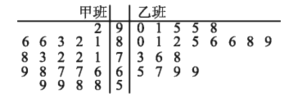
(1)从进入决赛的选手中随机抽出2名,X表示其中拥有“优先挑战权”的人数,求X的分布列和数学期望;
(2)请填写下面的![]() 列联表,并判断能否在犯错误的概率不超过0.025的前提下认为进入决赛与选择的导师有关?
列联表,并判断能否在犯错误的概率不超过0.025的前提下认为进入决赛与选择的导师有关?
甲班 | 乙班 | 合计 | |
进入决赛 | |||
未进入决赛 | |||
合计 |
下面的临界值表仅供参考:
P( | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: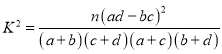 ,其中
,其中![]() )
)