题目内容
【题目】已知函数![]() (
(![]() 且
且![]() )
)
(1)若![]() 在定义域内单调递增,求实数a的取值范围;
在定义域内单调递增,求实数a的取值范围;
(2)若![]() 有两个不同的极值点
有两个不同的极值点![]() ,记过点
,记过点![]() ,
,![]() 的直线的斜率为k,求证:
的直线的斜率为k,求证:![]() .
.
【答案】(1)![]() (2)证明见解析
(2)证明见解析
【解析】
(1)由![]() 在
在![]() 上恒成立,再转化为求函数最值.
上恒成立,再转化为求函数最值.
(2)由(1)知![]() 时函数有两个极值点
时函数有两个极值点![]() ,
,![]() ,不妨设
,不妨设![]() ,从而有
,从而有![]() ,求出
,求出![]() ,并凑配出
,并凑配出 ,这样只要证明
,这样只要证明![]() ,再利用函数在单调性可证明.
,再利用函数在单调性可证明.
解:![]() 定义域
定义域![]() ,
,
由![]() 在定义域内单调递增,等价于对任意
在定义域内单调递增,等价于对任意![]() ,都有
,都有![]() ,
,
即![]() 恒成立,而
恒成立,而![]() ,
,
故![]() ,又
,又![]() ,所以
,所以![]() .
.
(2)定义域![]() ,设
,设![]() ,其判别式
,其判别式![]() ,当
,当![]() 时,由(1)得由
时,由(1)得由![]() 在定义域内单调递增,无极值点,
在定义域内单调递增,无极值点,
当![]() 时,
时,![]() ,
,![]() 两根为
两根为![]() ,
,![]() ,当
,当![]() 时,
时,![]() 上;当
上;当![]() 时,
时,![]() ;当
;当![]() 时,
时,![]() .故
.故![]() 在
在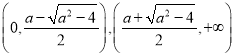 单调递增,在
单调递增,在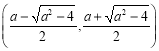 单调递减.即
单调递减.即![]() 是函数的极值点,不妨设
是函数的极值点,不妨设![]() ,
,![]() 则
则![]() 且
且![]() .
.
![]() ,所以
,所以
![]() ,而
,而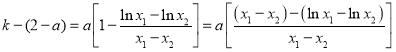 ,
,
而![]() 且
且![]() 得
得![]() ,故
,故![]() ,所以
,所以![]() ,
,![]() .
.
设![]() ,(
,(![]() ),而
),而![]() ,
,
所以![]() 在
在![]() 上单调递增,所以
上单调递增,所以![]() ,而
,而![]() ,故
,故![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目