题目内容
【题目】已知椭圆
过点
，且离心率为
．
（1）求椭圆
的标准方程；
（2）若点
与点
均在椭圆
上，且
关于原点对称，问：椭圆上是否存在点
（点
在一象限），使得
为等边三角形？若存在，求出点
的坐标；若不存在，请说明理由．
【答案】（1）
；（2）存在，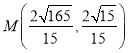
．
【解析】
试题分析：（1）根据已知条件，列出不等式组，求解
，即可求解椭圆的椭圆的方程；（2）设直线
的斜率为
，则直线
，代入椭圆的方程，解得
点的坐标，同理可得直线
的方程，代入求解所以
，即可求解点
的坐标．
试题解析：（1）由题意
，解得，
所以椭圆
的标准方程为．
（2）由题意知直线
经过坐标原点
，假设存在符合条件的点
，则直线
的斜率存在且大于零，
①
设直线的斜率为，则直线，
联立方程组
，得
，
所以
②
同理可得直线
的方程为
③
将②③代入①式得
，
化简得
，所以
所以，
综上所述，存在符合条件的点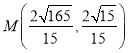
练习册系列答案
相关题目
【题目】某市
四所中学报名参加某高校今年自主招生的学生人数如下表所示：
中学 |
|
|
|
|
人数 |
|
|
|
|
为了了解参加考试的学生的学习状况，该高校采用分层抽样的方法从报名参加考试的四所中学的学生当中随机抽取50名参加问卷调查．
（1）问四所中学各抽取多少名学生？
（2）在参加问卷调查的
名学生中，从来自
两所中学的学生当中随机抽取两名学生，用
表示抽得
中学的学生人数，求
的分布列，数学期望和方差．
