题目内容
14.(1)计算:(-$\frac{1}{2}+\frac{\sqrt{3}}{2}$i)(1+i)=$-\frac{1}{2}-\frac{\sqrt{3}}{2}+(\frac{\sqrt{3}}{2}-\frac{1}{2})i$;(2)计算:$\frac{5(4+i)^{2}}{i(2+i)}$=1-38i.
分析 利用复数的运算法则分别化简计算.
解答 解:(1)原式=$-\frac{1}{2}+\frac{\sqrt{3}}{2}{i}^{2}+\frac{\sqrt{3}}{2}i-\frac{1}{2}i$=$-\frac{1}{2}-\frac{\sqrt{3}}{2}+(\frac{\sqrt{3}}{2}-\frac{1}{2})i$;
(2)原式=$\frac{5(15+8i)}{2i-1}$=$\frac{5(15+8i)(2i+1)}{(2i+1)(2i-1)}$=-$\frac{5(-1+38i)}{5}$=1-38i.
故答案为:(1)$-\frac{1}{2}-\frac{\sqrt{3}}{2}+(\frac{\sqrt{3}}{2}-\frac{1}{2})i$;(2)1-38i.
点评 本题考查了复数的混合运算;注意i2=-1.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
5.要得到函数y=sin(2x+$\frac{π}{5}$)的图象,只需将y=sin(x-$\frac{π}{5}$)的图象( )
| A. | 先向右平移$\frac{2π}{5}$个单位,再将横坐标缩小为原来的$\frac{1}{2}$倍 | |
| B. | 先向右平移$\frac{2π}{5}$个单位,再将横坐标扩大为原来的2倍 | |
| C. | 先向左平移$\frac{2π}{5}$个单位,再将横坐标缩小为原来的$\frac{1}{2}$倍 | |
| D. | 先向左平移$\frac{2π}{5}$个单位,再将横坐标扩大为原来的2倍 |
2.已知sinα-sinβ=$\frac{1}{2}$,cosα+cosβ=$\frac{1}{4}$,则cos(α+β)=( )
| A. | $\frac{1}{8}$ | B. | $\frac{3}{4}$ | C. | $\frac{5}{32}$ | D. | $-\frac{27}{32}$ |
19.已知a=3-2,b=0.3-2,c=log0.32,根据右边程序框图,输出的数是( )
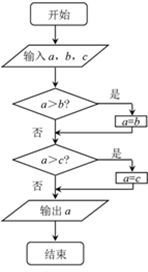

| A. | 3-2 | B. | 0.3-2 | C. | log0.32 | D. | 无法确定 |
3.设{an}是首项a1=1,公差为3的等差数列,如果an=2005,则序号n=( )
| A. | 667 | B. | 668 | C. | 669 | D. | 670 |
4.若函数f(x)=x2-2x,x∈[-2,4],则f(x)的值域为( )
| A. | [-1,8] | B. | [-1,16] | C. | [-2,8] | D. | [-2,4] |
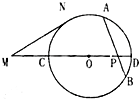 对于下列命题:
对于下列命题: