题目内容
4. 对于下列命题:
对于下列命题:①已知i是虚数单位,函数f(x)=$\left\{\begin{array}{l}\frac{1+i}{1-i}•i,(x>0)\\{a^x}-a,(x≤0)}&{\;}\end{array}\end{array}$在R上连续,则实数a=2.
②五本书排成一排,若A、B、C三本书左右顺序一定(不一定相邻),那么不同排法有A33•A33
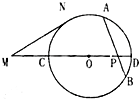
③如图,⊙O中的弦AB与直径CD相交于点p,M为DC延长线上一点,MN为⊙O的切线,N为切点,若AP=8,PB=6,PD=4,MC=6,则MN的长为2$\sqrt{33}$
④在极坐标系(ρ,θ)(0≤θ<2π)中,曲线ρ=2sinθ 与ρcosθ=-1交点的极坐标为($\sqrt{2}$,$\frac{3π}{4}$)
⑤设n=${∫}_{0}^{\frac{π}{2}}$4cosxdx,则二项式(x-$\frac{1}{x}$)n的展开式的常数项为6
其中假命题的序号是( )
| A. | ②⑤ | B. | ②③ | C. | ② | D. | ①④ |
分析 ①利用$\frac{1+i}{1-i}$•i=f(0),计算即可;
②采用插空法,依次插入即可;
③通过相交弦定理可得半径,利用勾股定理计算即可;
④利用平方关系可得ρ=$\sqrt{2}$,代回原式可得θ=$\frac{3}{4}$π,进而可得结论;
⑤通过定积分的性质可得n=4,代入计算即可.
解答 解:①$\frac{1+i}{1-i}$•i=$\frac{i-1}{1-i}$=-1,
f(0)=a0-a=1-a,
∵函数f(x)=$\left\{\begin{array}{l}\frac{1+i}{1-i}•i,(x>0)\\{a^x}-a,(x≤0)}&{\;}\end{array}\end{array}$在R上连续,
∴-1=1-a,即a=2,故正确;
②采用插空法,当A、B、C三本书左右顺序一定时(不一定相邻),
插入第4本书,有4中方法,
再插入第5本书,有5中方法,
∴不同排法有4×5=20种,故不正确;
③由相交弦定理可得:CP=$\frac{AP×PB}{PD}$=$\frac{8×6}{4}$=12,
∴圆O的半径为:$\frac{CP+PD}{2}$=$\frac{12+4}{2}$=8,
∵MN为⊙O的切线,
∴OM2=ON2+MN2,
∴MN2=OM2-ON2
=(OC+CM)2-ON2
=(8+6)2-82
=132,
∴MN=$\sqrt{132}$=2$\sqrt{33}$,故正确;
④∵ρ=2sinθ,ρcosθ=-1,
∴sinθ=$\frac{ρ}{2}$,cosθ=-$\frac{1}{ρ}$,
∴sin2θ+cos2θ=($\frac{ρ}{2}$)2+($\frac{1}{ρ}$)2=1,
整理得:${ρ}^{2}+\frac{4}{{ρ}^{2}}-4=0$,
解得:ρ=$\sqrt{2}$,
∴sinθ=$\frac{\sqrt{2}}{2}$,cosθ=-$\frac{\sqrt{2}}{2}$,
又∵0≤θ<2π,
∴θ=$\frac{3}{4}$π,
∴交点的极坐标为($\sqrt{2}$,$\frac{3π}{4}$),故正确;
⑤∵n=${∫}_{0}^{\frac{π}{2}}$4cosxdx=${∫}_{0}^{\frac{π}{2}}$4dsinx=4,
∴(x-$\frac{1}{x}$)4的展开式的常数项为${C}_{4}^{2}$=6,故正确;
综上所述,只有②是假命题,
故选:C.
点评 本题是一道综合题,考查复数、排列组合、平面几何、极坐标、定积分与展开式等基础知识,注意解题方法的积累,属于中档题.

 在平面直角坐标系中,圆O:x2+y2=4与x轴的正半轴交于点A,以A为圆心的圆A:(x-2)2+y2=r2(r>0)与圆O交于B,C两点.
在平面直角坐标系中,圆O:x2+y2=4与x轴的正半轴交于点A,以A为圆心的圆A:(x-2)2+y2=r2(r>0)与圆O交于B,C两点.