题目内容
设函数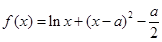 ,
,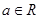 .
.
(1)若函数 在
在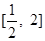 上单调递增,求实数
上单调递增,求实数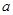 的取值范围;
的取值范围;
(2)求函数 的极值点.
的极值点.
(3)设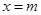 为函数
为函数 的极小值点,
的极小值点,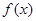 的图象与
的图象与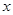 轴交于
轴交于 两点,且
两点,且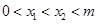 ,
,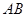 中点为
中点为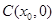 ,
,
求证: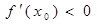 .
.
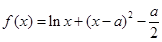 ,
,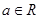 .
.(1)若函数
 在
在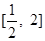 上单调递增,求实数
上单调递增,求实数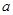 的取值范围;
的取值范围;(2)求函数
 的极值点.
的极值点.(3)设
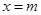 为函数
为函数 的极小值点,
的极小值点,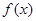 的图象与
的图象与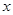 轴交于
轴交于 两点,且
两点,且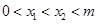 ,
,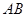 中点为
中点为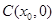 ,
,求证:
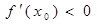 .
.(1)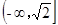 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.
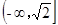 ;(2)详见解析;(3)详见解析.
;(2)详见解析;(3)详见解析.试题分析:(1)先求
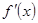 ,在
,在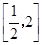 上
上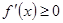 恒成立,反解参数
恒成立,反解参数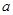 ,转化成
,转化成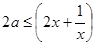 恒成立问题,利用基本不等式求
恒成立问题,利用基本不等式求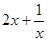 的最小值问题;
的最小值问题;(2)先求函数的导数,因为
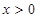 ,所以设
,所以设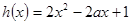 ,分情况讨论
,分情况讨论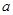 在不同情况下,
在不同情况下,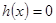 的根,通过
的根,通过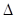 来讨论,主要分
来讨论,主要分 以及
以及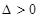 的情况,求出导数为0的值,判断两侧的单调性是否改变,从而确定极值点;
的情况,求出导数为0的值,判断两侧的单调性是否改变,从而确定极值点;(3)
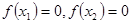 ,两式相减,结合中点坐标公式,
,两式相减,结合中点坐标公式,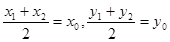 ,表示出
,表示出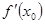 ,设出
,设出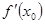 的能表示正负的部分函数,再求导数,利用导数得出单调性,从而确定
的能表示正负的部分函数,再求导数,利用导数得出单调性,从而确定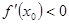 .
.试题解析:(1)
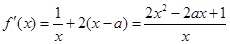
依题意得,在区间
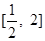 上不等式
上不等式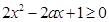 恒成立.
恒成立.又因为
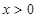 ,所以
,所以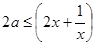 .所以
.所以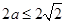 ,
,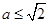
所以实数
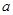 的取值范围是
的取值范围是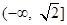 . 2分
. 2分(2)
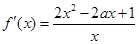 ,令
,令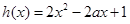
①显然,当
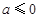 时,在
时,在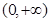 上
上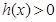 恒成立,这时
恒成立,这时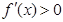 ,此时,函数
,此时,函数 没有极值点; ..3分
没有极值点; ..3分②当
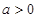 时,
时,(ⅰ)当
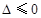 ,即
,即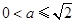 时,在
时,在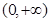 上
上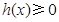 恒成立,这时
恒成立,这时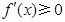 ,此时,函数
,此时,函数 没有极值点; .4分
没有极值点; .4分(ⅱ)当
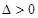 ,即
,即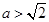 时,
时,易知,当
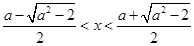 时,
时,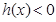 ,这时
,这时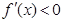 ;
;当
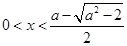 或
或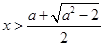 时,
时,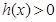 ,这时
,这时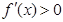 ;
;所以,当
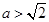 时,
时,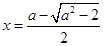 是函数
是函数 的极大值点;
的极大值点;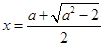 是函数
是函数 的极小值点.
的极小值点.综上,当
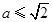 时,函数
时,函数 没有极值点; .6分
没有极值点; .6分当
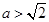 时,
时,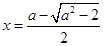 是函数
是函数 的极大值点;
的极大值点;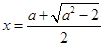 是函数
是函数 的极小值点. 8分
的极小值点. 8分(Ⅲ)由已知得
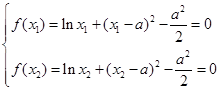 两式相减,
两式相减,得:
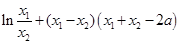 ①
①由
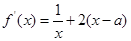 ,得
,得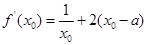 ②得①代入②,得
②得①代入②,得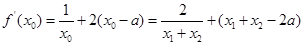
=
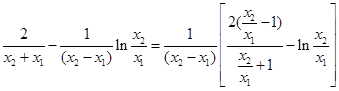 10分
10分令
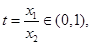 且
且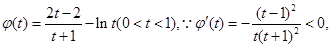
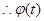 在
在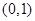 上递减,
上递减,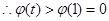
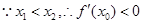 12分
12分
练习册系列答案
相关题目
 .
. ,
,  的单调区间;
的单调区间; 内存在
内存在 ,使不等式
,使不等式 成立,求
成立,求 的取值范围.
的取值范围. 是减函数的区间为 ( )
是减函数的区间为 ( )



 有两个极值点
有两个极值点 ,且
,且 ,
, ,则( )
,则( )



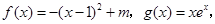 若
若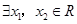 ,使得
,使得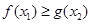 成立,则实数
成立,则实数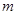 的取值范围是_______.
的取值范围是_______. ,函数
,函数 ,若
,若 在
在 上是单调减函数,则
上是单调减函数,则 的取值范围是
的取值范围是



 的单调递增区间是
的单调递增区间是