题目内容
已知函数 ,
,
(1)求函数 的单调区间;
的单调区间;
(2)在区间 内存在
内存在 ,使不等式
,使不等式 成立,求
成立,求 的取值范围.
的取值范围.
 ,
, (1)求函数
 的单调区间;
的单调区间;(2)在区间
 内存在
内存在 ,使不等式
,使不等式 成立,求
成立,求 的取值范围.
的取值范围.(1)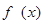 的单调递增区间是
的单调递增区间是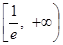 ,
,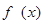 的单调递减区间是
的单调递减区间是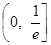 .
.
(2) 的取值范围是
的取值范围是 .
.
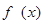 的单调递增区间是
的单调递增区间是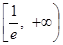 ,
,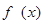 的单调递减区间是
的单调递减区间是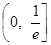 .
.(2)
 的取值范围是
的取值范围是 .
.试题分析:(1)首先确定函数的定义域.求导数:
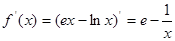 ,根据当
,根据当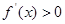 时,
时,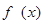 为单调递增函数;
为单调递增函数;当
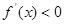 时,
时,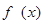 为单调递减函数,得到函数的单调区间.
为单调递减函数,得到函数的单调区间.(2)构造函数
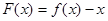 ,即
,即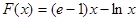 ,将问题转化成:在区间
,将问题转化成:在区间 内,
内,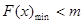 ,利用导数求函数的极值、最小值,得到
,利用导数求函数的极值、最小值,得到 的取值范围是
的取值范围是 .
.试题解析:(1)函数
 的定义域为
的定义域为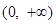 ,
,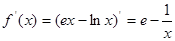 2分
2分当
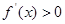 ,即
,即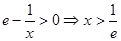 时,
时,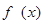 为单调递增函数;
为单调递增函数;当
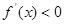 ,即
,即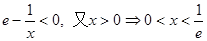 时,
时,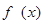 为单调递减函数;
为单调递减函数;所以,
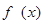 的单调递增区间是
的单调递增区间是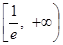 ,
,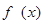 的单调递减区间是
的单调递减区间是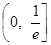 6分
6分(2)由不等式
 ,得
,得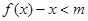 ,令
,令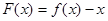 ,
,则
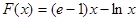 8分
8分由题意可转化为:在区间
 内,
内,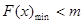 ,
,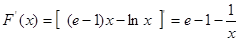 ,令
,令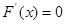 ,得
,得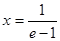
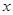 | 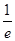 | 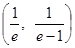 | 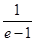 | 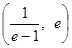 | 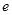 |
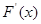 | | | 0 | + | |
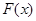 | | 递减 | 极小值 | 递增 | |
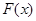 的极小值是
的极小值是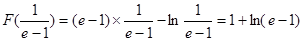 且唯一,
且唯一,所以
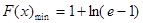 。 10分
。 10分因此,所求
 的取值范围是
的取值范围是 . 13分
. 13分
练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
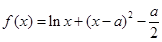 ,
,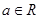 .
. 在
在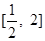 上单调递增,求实数
上单调递增,求实数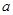 的取值范围;
的取值范围;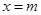 为函数
为函数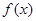 的图象与
的图象与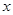 轴交于
轴交于 两点,且
两点,且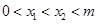 ,
,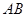 中点为
中点为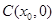 ,
,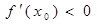 .
.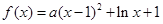 .
.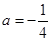 时,求函数
时,求函数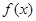 的极值;
的极值;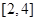 上是减函数,求实数
上是减函数,求实数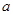 的取值范围;
的取值范围;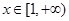 时,函数
时,函数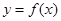 图像上的点都在
图像上的点都在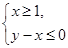 所表示的平面区域内,求实数
所表示的平面区域内,求实数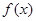 为
为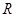 上的可导函数,且
上的可导函数,且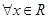 ,均有
,均有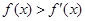 ,则以下判断正确的是
,则以下判断正确的是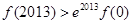
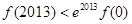
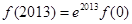
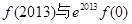 大小无法确定
大小无法确定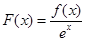 是定义在
是定义在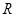 上的函数,其中
上的函数,其中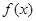 的导函数为
的导函数为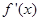 ,满足
,满足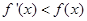 对于
对于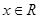 恒成立,则
恒成立,则



 的单调递增区间是_____________.
的单调递增区间是_____________.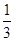 x3-
x3-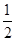 ax2+(a-1)x+1在区间(1,4)上是减函数,在区间(6,+∞)上是增函数,则实数a的取值范围是________.
ax2+(a-1)x+1在区间(1,4)上是减函数,在区间(6,+∞)上是增函数,则实数a的取值范围是________.